题目内容
已知圆C过点p(0,2,)O(0,0),Q(4,0)三点:
(Ⅰ)求圆C的方程;
(Ⅱ)过点A(2,2)的直线l与圆C交于M,N两点,且|MN|=4,求直线l方程.
(Ⅰ)求圆C的方程;
(Ⅱ)过点A(2,2)的直线l与圆C交于M,N两点,且|MN|=4,求直线l方程.
考点:直线与圆的位置关系,圆的一般方程
专题:直线与圆
分析:(Ⅰ)根据题意可得,△POQ是直角三角形,所以过这三点的圆C是以PQ为直径的圆.从而可求出圆心和半径,进而求出圆的方程.
(Ⅱ)设直线l的斜率为k,分k不存在和存在两种情况讨论.当k不存在时,直线方程为x=2,此时|MN|=2
,不满足条件.当k存在时,利用弦长公式以及点直线的距离公式即可得到k=0.从而求出直线方程.
(Ⅱ)设直线l的斜率为k,分k不存在和存在两种情况讨论.当k不存在时,直线方程为x=2,此时|MN|=2
| 5 |
解答:
解:(Ⅰ)由题意得,△POQ显然是直角三角形,
∴过这三点的圆C是以PQ为直径的圆.
∴圆心C(2,1),半径为
.
∴圆C的方程为(x-2)2+(y-1)2=5.
(Ⅱ)设直线l的斜率为k,
(1)当k不存在时,直线l的方程为x=2.
则M(2,1+
),N(2,1-
).
|MN|=2
,不满足条件.
(2)当k存在时,设直线l为y-2=k(x-2).
即kx-y-2k+2=0.
圆心C到直线l的距离d=
=
=1.
解得k=0.
∴直线l的方程为y=2.
综上所述,直线l的方程为y=2.
∴过这三点的圆C是以PQ为直径的圆.
∴圆心C(2,1),半径为
| 5 |
∴圆C的方程为(x-2)2+(y-1)2=5.
(Ⅱ)设直线l的斜率为k,
(1)当k不存在时,直线l的方程为x=2.
则M(2,1+
| 5 |
| 5 |
|MN|=2
| 5 |
(2)当k存在时,设直线l为y-2=k(x-2).
即kx-y-2k+2=0.
圆心C到直线l的距离d=
| |2k-1-2k+2| | ||
|
| 5-22 |
解得k=0.
∴直线l的方程为y=2.
综上所述,直线l的方程为y=2.
点评:本题考查圆的标准方程,点到直线的距离公式,直线与圆相交的性质等知识,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
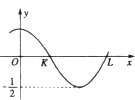 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(| 1 |
| 6 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、
|