题目内容
定义域为R的函数f(x)满足f(x+2)=f(x),当x∈[0,2]时,f(x)=x2-2x
(1)当x∈[-4,-2]时,求f(x)的解析式;
(2)当x∈[-4,-2]时,f(x)≥
(
-t)恒成立,求实数t的取值范围.
(1)当x∈[-4,-2]时,求f(x)的解析式;
(2)当x∈[-4,-2]时,f(x)≥
| 1 |
| 2 |
| 3 |
| t |
考点:函数恒成立问题,函数的周期性
专题:综合题,函数的性质及应用
分析:(1)先设x∈[-4,-2],则x+4∈[0,2],结合已知当x∈[0,2]时,f(x)=x2-2x可求f(x+4),由f(x+4)=f(x+2)=f(x),代入可求f(x);
(2)由x∈[-4,-2]时,f(x)=x2+6x+8=(x+3)2-1,结合而成函数的性质可求f(x)的最小值,而由f(x)≥
(
-t)恒成立,可得f(x)min≥
(
-t),解不等式可求t的范围.
(2)由x∈[-4,-2]时,f(x)=x2+6x+8=(x+3)2-1,结合而成函数的性质可求f(x)的最小值,而由f(x)≥
| 1 |
| 2 |
| 3 |
| t |
| 1 |
| 2 |
| 3 |
| t |
解答:
解:(1)设x∈[-4,-2],则x+4∈[0,2],
∵当x∈[0,2]时,f(x)=x2-2x,
∴f(x+4)=(x+4)2-2(x+4)=x2+6x+8,
又∵f(x+2)=f(x),
∴f(x+4)=f(x+2)=f(x),
∴f(x)=x2+6x+8;
(2)∵x∈[-4,-2]时,f(x)=x2+6x+8=(x+3)2-1,
当x=-3时,f(x)min=f(-3)=-1
则由f(x)≥
(
-t)恒成立,可得-1≥
(
-t)恒成立,
整理可得,
≤0
∴-1≤t<0或t≥3.
∵当x∈[0,2]时,f(x)=x2-2x,
∴f(x+4)=(x+4)2-2(x+4)=x2+6x+8,
又∵f(x+2)=f(x),
∴f(x+4)=f(x+2)=f(x),
∴f(x)=x2+6x+8;
(2)∵x∈[-4,-2]时,f(x)=x2+6x+8=(x+3)2-1,
当x=-3时,f(x)min=f(-3)=-1
则由f(x)≥
| 1 |
| 2 |
| 3 |
| t |
| 1 |
| 2 |
| 3 |
| t |
整理可得,
| (t+1)(t-3) |
| t |
∴-1≤t<0或t≥3.
点评:本题主要考查了利用已知抽象函数的关系求解函数的解系式,解题的关键是由已知推出f(x+4)=f(x),而函数的恒成立问题往往转化为函数的最值的求解,属于中档题.

练习册系列答案
相关题目
已知集合A={-1,1,3},B={1,3,5},则A∪B=( )
| A、{-1,1,3,5} |
| B、{1,3} |
| C、{-1,5} |
| D、{-1,1,1,3,3,5} |
已知向量
=(-2,5)与向量
=(λ,2)不共线,又函数f(x)=(x
+
)•(
-x
)在(0,+∞)有最大值,则λ的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、λ<5 | ||
| B、-5<λ<5 | ||
C、λ<5,且λ≠-
| ||
D、-5<λ<5,且λ≠-
|
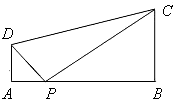 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.