题目内容
某学生邀请10位同学中的6位参加一项活动,其中两位同学要么都请,要么都不请,共有 邀请方案.(用数字回答)
考点:计数原理的应用
专题:应用题,排列组合
分析:根据题意,这2位同学要么都参加,要么都不参加,则分两种情况讨论:①、若2位同学都参加,只需从剩余的8人中再取出4人参加,②、若2位同学都不参加,只需从剩余的8人中取出6人参加,由组合公式计算可得其情况数目,由分类计数原理,计算可得答案.
解答:
解:根据题意,分两种情况讨论:
①、2位同学都参加,只需从剩余的8人中再取出4人参加,有C84=70种选派方法,
②、2位同学都不参加,只需从剩余的8人中取出6人参加,有C86=28种选派方法,
共有70+28=98种;
故答案为:98
①、2位同学都参加,只需从剩余的8人中再取出4人参加,有C84=70种选派方法,
②、2位同学都不参加,只需从剩余的8人中取出6人参加,有C86=28种选派方法,
共有70+28=98种;
故答案为:98
点评:本题考查排列、组合的应用,是简单题,注意分类讨论、正确计算即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}满足an+2-an+1=an+1-an,n∈N*,且a5=
,若函数f(x)=sin2x+2cos2
,记yn=f(an),则数列{yn}的前9项和为( )
| π |
| 2 |
| x |
| 2 |
| A、0 | B、-9 | C、9 | D、1 |
已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长( )
A、
| ||
B、
| ||
| C、29 | ||
D、
|
已知f(x)是定义在实数集R上的奇函数,且f(x+4)=f(x) 当x∈(0,2)时,f(x)=2x2,则f(2011)=( )
| A、98 | B、-98 | C、2 | D、-2 |
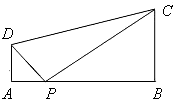 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β. 
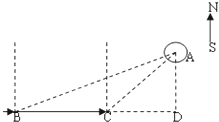 海中一小岛,周围3.8mile内有暗礁,海轮由西向东航行,望见这岛在北偏东80°,航行8n mile以后,望见这岛在北偏东60°,如查这艘海轮不改变航行继续前进,有没有触礁的危险.(精确到0.001,cos10°=0.9848)
海中一小岛,周围3.8mile内有暗礁,海轮由西向东航行,望见这岛在北偏东80°,航行8n mile以后,望见这岛在北偏东60°,如查这艘海轮不改变航行继续前进,有没有触礁的危险.(精确到0.001,cos10°=0.9848)