题目内容
已知F1,F2是椭圆的焦点,P为椭圆上一点,∠F1PF2=60°.
(1)求椭圆离心率的取值范围;
(2)求证:△F1PF2的面积只与椭圆的短轴长有关.
(1)求椭圆离心率的取值范围;
(2)求证:△F1PF2的面积只与椭圆的短轴长有关.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意,可设|PF1|=m,|PF2|=n. 在△PF1F2中,由余弦定理可知,4c2=m2+n2-2mncos60°.再由定义得出m+n=2a,然后进行恒等变形,将4c2=m2+n2-2mncos60°量m,n用a,c表示出来即可得出离心率的取值范围
(2)根据(1)中的结论,可算出△F1PF2的面积等于
b2,由此可得△F1PF2的面积仅与椭圆的短轴长有关.
(2)根据(1)中的结论,可算出△F1PF2的面积等于
| ||
| 3 |
解答:
解:设椭圆方程为
+
=1(a>b>0),|PF1|=m,|PF2|=n.
在△PF1F2中,由余弦定理可知,4c2=m2+n2-2mncos60°.
∵m+n=2a,∴m2+n2=(m+n)2-2mn=4a2-2mn,
∴4c2=4a2-3mn.即3mn=4a2-4c2.
又mn≤(
)2=a2(当且仅当m=n时取等号),
∴4a2-4c2≤3a2,∴
≥
,即e≥
.
∴e的取值范围是[
,1).
(2)由(1),得mn=
=
b2,
∴S△F1PF2=
mnsin60°=
b2,
面积表达式中的字母只含有b,可得:△F1PF2的面积只与椭圆的短轴长有关.
| x2 |
| a2 |
| y2 |
| b2 |
在△PF1F2中,由余弦定理可知,4c2=m2+n2-2mncos60°.
∵m+n=2a,∴m2+n2=(m+n)2-2mn=4a2-2mn,
∴4c2=4a2-3mn.即3mn=4a2-4c2.
又mn≤(
| m+n |
| 2 |
∴4a2-4c2≤3a2,∴
| c2 |
| a2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴e的取值范围是[
| 1 |
| 2 |
(2)由(1),得mn=
| 4(a2-c2) |
| 3 |
| 4 |
| 3 |
∴S△F1PF2=
| 1 |
| 2 |
| ||
| 3 |
面积表达式中的字母只含有b,可得:△F1PF2的面积只与椭圆的短轴长有关.
点评:本题给出椭圆上一点与椭圆两个焦点构成的三角形,求三角形的面积并讨论椭圆的离心率,着重考查了椭圆的定义与简单性质、基本不等式求最值和用正余弦定理解三角形等知识,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
若等差数列{an}中有a2+a4024=4,则a2013=( )
| A、2 | B、4 | C、3 | D、6 |
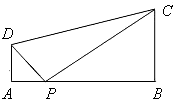 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.