题目内容
对于函数f(x):如果对任意x1,x2∈(0,+∞)且x1≠x2,都有f(
)≤
[f(x 1)+f(x2)],那么称函数f(x)是(0,+∞)上的凹函数.现有函数:(1)f(x)=x2;(2)f(x)=2x+1;(3)f(x)=log2(x+1),以上哪些函数在(0,+∞)上是凹函数,请写出相应的序号 .
| x1+x2 |
| 2 |
| 1 |
| 2 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:对于(1),把f(
),
[f(x1)+f(x2)]代入f(x)=x2,整理后利用基本不等式得到f(
)≤
[f(x 1)+f(x2)],说明函数f(x)=x2是(0,+∞)上的凹函数;
对于(2),把f(
),
[f(x1)+f(x2)]代入f(x)=2x+1,整理后利用基本不等式得到f(
)≤
[f(x 1)+f(x2)],说明函数f(x)=2x+1是(0,+∞)上的凹函数;
对于(3),利用基本不等式结合对数函数的运算性质得到g(x)不是(0,+∞)上的凹函数,然后由函数图象的平移得答案.
| x1+x2 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
对于(2),把f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
对于(3),利用基本不等式结合对数函数的运算性质得到g(x)不是(0,+∞)上的凹函数,然后由函数图象的平移得答案.
解答:
解:对于(1),f(x)=x2,
f(
)=(
)2=
(x12+2x1x2+x22)<
(2x12+2x22)=
(x12+x22),
而
[f(x1+x2)]=
(x12+x22),
∴f(
)≤
[f(x 1)+f(x2)],
函数f(x)=x2是(0,+∞)上的凹函数;
对于(2),f(x)=2x+1,
f(
)=2
+1=2
,
[f(x1+x2)]=
(2x1+1+2x2+1)>
•2
=2
,
∴f(
)≤
[f(x 1)+f(x2)],
函数f(x)=2x+1是(0,+∞)上的凹函数;
对于(3),f(x)=log2(x+1),
令g(x)=log2x,
g(
)=log2
>log2
.
[g(x1)+g(x2)]=
(log2x1+log2x2)=
log2x1x2=log2
.
∴g(x)不是(0,+∞)上的凹函数.
而f(x)=g(x+1),
∴f(x)不是(0,+∞)上的凹函数.
∴正确命题的序号是(1)(2).
故答案为:(1)(2).
f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
而
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
函数f(x)=x2是(0,+∞)上的凹函数;
对于(2),f(x)=2x+1,
f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2+2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2x1+1•2x2+1 |
| x1+x2+2 |
| 2 |
∴f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
函数f(x)=2x+1是(0,+∞)上的凹函数;
对于(3),f(x)=log2(x+1),
令g(x)=log2x,
g(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1x2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x1x2 |
∴g(x)不是(0,+∞)上的凹函数.
而f(x)=g(x+1),
∴f(x)不是(0,+∞)上的凹函数.
∴正确命题的序号是(1)(2).
故答案为:(1)(2).
点评:本题考查了幂函数、指数函数以及对数函数的运算性质,考查了基本不等式的用法,是新定义题,解答的关键是对题意的理解,是中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
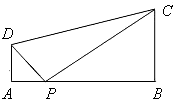 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.