题目内容
已知A(-2,4),B(2,8)是直线y=x+6上两点,若线段AB与椭圆
+
=1有公共点,则正数a的取值范围是 .
| x2 |
| a2 |
| y2 |
| a2-4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:联立
,化为(2a2-4)x2+12a2x+40a2-a4=0,令△=0,及a2>4,解得x=-
.由于-
<-2<2.可得:切点在线段AB之外.因此把A(-2,4),B(2,8)分别代入椭圆的标准方程即可得出.
|
| 10 |
| 3 |
| 10 |
| 3 |
解答:
解:联立
,化为(2a2-4)x2+12a2x+40a2-a4=0,(*)
令△=0,及a2>4,解得a2=20.
方程(*)(3x+10)2=0,解得x=-
.
∵-
<-2<2.
∴切点在线段AB之外.
因此把A(-2,4)代入椭圆方程可得
+
=1,及a2>4,解得a=2
+2.
把B(2,8)代入椭圆方程可得
+
=1,及a2>4,解得a=2
+4.
由于线段AB与椭圆
+
=1有公共点,因此正数a的取值范围是[2
+2,4+2
].
故答案为:[2
+2,4+2
].
|
令△=0,及a2>4,解得a2=20.
方程(*)(3x+10)2=0,解得x=-
| 10 |
| 3 |
∵-
| 10 |
| 3 |
∴切点在线段AB之外.
因此把A(-2,4)代入椭圆方程可得
| 4 |
| a2 |
| 16 |
| a2-4 |
| 2 |
把B(2,8)代入椭圆方程可得
| 4 |
| a2 |
| 64 |
| a2-4 |
| 5 |
由于线段AB与椭圆
| x2 |
| a2 |
| y2 |
| a2-4 |
| 2 |
| 5 |
故答案为:[2
| 2 |
| 5 |
点评:本题考查了直线及其点与椭圆的位置关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
若等差数列{an}中有a2+a4024=4,则a2013=( )
| A、2 | B、4 | C、3 | D、6 |
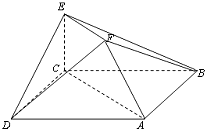 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=| 2 |
(1)求证:平面BEF⊥平面DEF;
(2)求二面角A-BF-E的余弦值.
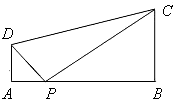 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β. 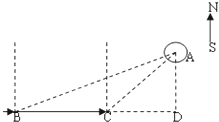 海中一小岛,周围3.8mile内有暗礁,海轮由西向东航行,望见这岛在北偏东80°,航行8n mile以后,望见这岛在北偏东60°,如查这艘海轮不改变航行继续前进,有没有触礁的危险.(精确到0.001,cos10°=0.9848)
海中一小岛,周围3.8mile内有暗礁,海轮由西向东航行,望见这岛在北偏东80°,航行8n mile以后,望见这岛在北偏东60°,如查这艘海轮不改变航行继续前进,有没有触礁的危险.(精确到0.001,cos10°=0.9848)