题目内容
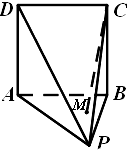如图，四棱锥P-ABCD的底面ABCD是边长为1的正方形，面PAB⊥面ABCD．在面PAB内的有一个动点M，记M到面PAD的距离为d．若|MC|2-d2=1，则动点M在面PAB内的轨迹是（ ）| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
考点：抛物线的定义,双曲线的定义
专题：圆锥曲线的定义、性质与方程
分析：根据面面垂直的性质推断出即点M到直线AD的距离，即为点M到平面PAD的距离，进而根据抛物线的定义推断出点M的轨迹为抛物线．
解答：
解：∵侧面PAD与底面ABCD垂直，且AD为二面的交线，
∴点M向AP作垂线，垂线一定垂直于平面PAD，
即点M到直线AP的距离，即为点M到平面PAD的距离，
∴动点M到点C的距离等于点M直线的距离，
根据抛物线的定义可知，M点的轨迹为抛物线．
故答案为：抛物线．
∴点M向AP作垂线，垂线一定垂直于平面PAD，
即点M到直线AP的距离，即为点M到平面PAD的距离，
∴动点M到点C的距离等于点M直线的距离，
根据抛物线的定义可知，M点的轨迹为抛物线．
故答案为：抛物线．
点评：本题主要考查了平面与平面垂直的性质．在平面与平面垂直的问题上，要特别注意两面的交线．
练习册系列答案
相关题目
下列三个图象中能表示y是x的函数图象的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
函数y=（
）x2-2的单调递减区间为（ ）
| 1 |
| 2 |
| A、（-∞，0] | ||
| B、[0，+∞） | ||
C、（-∞，
| ||
D、[
|