题目内容
设f：x→-2x2+3x是集合A=R到集合B=R的映射，若对于实数p∈B，在A中不存在对应的元素，则实数p的取值范围是 ．
考点：映射
专题：函数的性质及应用
分析：先将二次函数进行配方，求出二次函数的值域，然后求出值域的补集即为p的取值范围．
解答：
解：∵y=-2x2+3x=-2（x-
）2+
≤
，
∴函数的值域为（-∞，
]
∵对于实数p∈B，在集合A中不存在原象
∴p＞
，
故答案为：p＞
| 3 |
| 4 |
| 9 |
| 8 |
| 9 |
| 8 |
∴函数的值域为（-∞，
| 9 |
| 8 |
∵对于实数p∈B，在集合A中不存在原象
∴p＞
| 9 |
| 8 |
故答案为：p＞
| 9 |
| 8 |
点评：本题主要考查了映射，以及利用配方法求二次函数的值域，属于基础题．
练习册系列答案
相关题目
下列函数中为偶函数的是（ ）
| A、y=x2+1（x∈R） |
| B、y=（x+1）2（x∈R） |
| C、y=x2+1（x＞0） |
| D、y=-x2+1（x＞0） |
已知函数f（x）=xa，且满足f（9）=3，则f（100）=（ ）
| A、10 | B、100 |
| C、1000 | D、10000 |
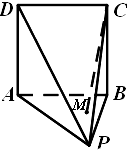如图，四棱锥P-ABCD的底面ABCD是边长为1的正方形，面PAB⊥面ABCD．在面PAB内的有一个动点M，记M到面PAD的距离为d．若|MC|2-d2=1，则动点M在面PAB内的轨迹是（ ）| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
直线l不经过坐标原点O，且与椭圆
+y2=1交于A、B两点，M是线段AB的中点．那么，直线AB与直线OM的斜率之积为（ ）
| x2 |
| 2 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
| D、2 |