题目内容
已知{an}是首项为a,公差不为零的等差数列,{an}的部分项a k1、a k2、…、a kn恰好为等比数列,且k1=1,k2=5,k3=17.
(1)求数列{an}和{kn}的通项公式;
(2)设数列{kn}的前n项和为Sn求证:
+
+…+
<
.
(1)求数列{an}和{kn}的通项公式;
(2)设数列{kn}的前n项和为Sn求证:
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 3 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)设数列{an}的公差为d,由已知得2d2=ad,所以d=
.an=a1+(n-1)d=
a.akn=
a,而等比数列{a kn}的公比q=
=
=3,由此能求出kn=2×3n-1-1.
(2)由(1)知,Sn=3n-n-1.由二项式定理推导出3n-n-1>2n,n≥2.所以
=
<
,n≥2.由此能证明
+
+…+
<
.
| a |
| 2 |
| n+1 |
| 2 |
| kn+1 |
| 2 |
| a5 |
| a1 |
| 3a |
| a |
(2)由(1)知,Sn=3n-n-1.由二项式定理推导出3n-n-1>2n,n≥2.所以
| 1 |
| Sn |
| 1 |
| 3n-n-1 |
| 1 |
| 2n |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 3 |
| 2 |
解答:
解:(1)设数列{an}的公差为d,
由已知得a1=a,a5=a+4d,a17=a+16成等比数列,
∴(a+4d)2=a(a+16d),即2d2=ad.
∵d≠0,∴d=
.
∴an=a1+(n-1)d=a+(n-1)•
=
a.
∴akn=
a,而等比数列{a kn}的公比q=
=
=3,
∴akn=a1•3n-1=a•3n-1,
故
a=a•3n-1.
由a1=a≠0,得kn=2×3n-1-1.
(2)由(1)知,Sn=2×(1+3+32+…+3n-1)-n
=
-n=3n-n-1.
∵当n>1时,3n=(1+2)n=
×2+
×22+…+
×2n-1
×2n
≥
×2+
×2n
=2n+2n+1>2n+n+1,
∴3n-n-1>2n,n≥2.
∴
=
<
,n≥2.
∴当n≥2时,
+
+…+
<1+
+
+
+…+
=1+
=
-(
)n<
.
当n=1时,左边=
=1<
,不等式也成立.
综上所述,
+
+…+
<
.
由已知得a1=a,a5=a+4d,a17=a+16成等比数列,
∴(a+4d)2=a(a+16d),即2d2=ad.
∵d≠0,∴d=
| a |
| 2 |
∴an=a1+(n-1)d=a+(n-1)•
| a |
| 2 |
| n+1 |
| 2 |
∴akn=
| kn+1 |
| 2 |
| a5 |
| a1 |
| 3a |
| a |
∴akn=a1•3n-1=a•3n-1,
故
| kn+1 |
| 2 |
由a1=a≠0,得kn=2×3n-1-1.
(2)由(1)知,Sn=2×(1+3+32+…+3n-1)-n
=
| 2(1-3n) |
| 1-3 |
∵当n>1时,3n=(1+2)n=
| C | 0 n |
| +C | 1 n |
| C | 2 n |
| C | n-1 n |
| +C | n n |
≥
| C | 0 n |
| +C | 1 n |
| C | n n |
=2n+2n+1>2n+n+1,
∴3n-n-1>2n,n≥2.
∴
| 1 |
| Sn |
| 1 |
| 3n-n-1 |
| 1 |
| 2n |
∴当n≥2时,
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
=1+
| ||||
1-
|
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当n=1时,左边=
| 1 |
| S1 |
| 3 |
| 2 |
综上所述,
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 3 |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意二项式定理的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
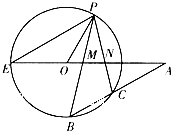 如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.
如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.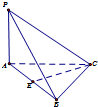 如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2
如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2