题目内容
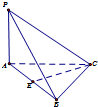 如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2
如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2| 5 |
(Ⅰ)求证:PA⊥平面ABC;
(Ⅱ)若E为AB的中点,求直线CE与平面PAB所成角的余弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明PA⊥AB,利用PA⊥BC,AB∩BC=B,即可证明PA⊥平面ABC;
(Ⅱ)求出C到平面PAB的距离,CE,即可求直线CE与平面PAB所成角的余弦值.
(Ⅱ)求出C到平面PAB的距离,CE,即可求直线CE与平面PAB所成角的余弦值.
解答:
(Ⅰ)证明:∵AB=2,AP=4,PB=2
,
∴AB2+AP2=PB2,∴PA⊥AB,
∵PA⊥BC,AB∩BC=B,
∴PA⊥平面ABC;
(Ⅱ)解:设C到平面PAB的距离为h,直线CE与平面PAB所成角为α,则
由等体积可得
•
•4•2•sin60°=
•
•4•2•h,
∴h=
,
∵E为AB的中点,
∴CE=
=
,
∴sinα=
=
,
∴cosα=
.
| 5 |
∴AB2+AP2=PB2,∴PA⊥AB,
∵PA⊥BC,AB∩BC=B,
∴PA⊥平面ABC;
(Ⅱ)解:设C到平面PAB的距离为h,直线CE与平面PAB所成角为α,则
由等体积可得
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
| ||
| 2 |
∵E为AB的中点,
∴CE=
| 1+12 |
| 13 |
∴sinα=
| ||||
|
| ||
2
|
∴cosα=
7
| ||
| 26 |
点评:本题考查线面垂直,考查线面角,正确运用线面垂直的判定定理是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
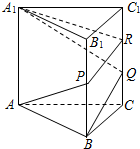 已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=
已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=