题目内容
设{an}是公差不为零的等差数列,Sn为其前n项和,满足:a22+a32=a42+a52,S7=7.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的及前n项和Tn;
(3)试求所有的正整数m,使得
为数列{an}中的项.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的及前n项和Tn;
(3)试求所有的正整数m,使得
| amam+1 |
| am+2 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)设公差为d,由已知条件利用等差数列的通项公式和前n项和公式求出首项和公差,由此能求出数列{an}的通项公式.
(2)由(1)知,当n≤3时,an<0;当n>3时,an>0.Sn=
=
=n2-6n.由此能求出数列{|an|}的及前n项和Tn.
(3)
=
,令2m-3=t,则
=
=t+
-6.由此能求出满足条件的正整数m=2.
(2)由(1)知,当n≤3时,an<0;当n>3时,an>0.Sn=
| n(a1+an) |
| 2 |
| n(-5+2n-7) |
| 2 |
(3)
| amam+1 |
| am+2 |
| (2m-7)(2m-5) |
| 2m-3 |
| amam+1 |
| am+2 |
| (t-4)(t-2) |
| t |
| 8 |
| t |
解答:
解:(1)设公差为d,则
-
=
-
,
由等差数列性质得-3d(a4+a3)=d(a4+a3).
因为d≠0,所以
+
=0,即2a1+5d=0①.
又由S7=7得7a1+
d=7,即a1+3d②.
联立①②解得a1=-5,d=2,
所以an=2n-7(n∈N*).
(2)由(1)知,当n≤3时,an<0;
当n>3时,an>0.
Sn=
=
=n2-6n.
∴当n≤3时,Tn=-Sn=-n2+6n;
当n>3时,Tn=-S3+(Sn-S3)=Sn-2S3=(n2-6n)-2×(-9)=n2-6n+18.
综上,Tn=
.
(3)
=
,
令2m-3=t,则
=
=t+
-6.
故t为8的约数,又∵t是奇数,∴t的可能取值为±1.
当t=1时,m=2,
=3=2×5-7是数列{an}中的第5项;
当t=-1时,m=1,
=-15=2×(-4)-7不是数列{an}中的项.
所以满足条件的正整数m=2.
| a | 2 2 |
| a | 2 5 |
| a | 2 4 |
| a | 2 3 |
由等差数列性质得-3d(a4+a3)=d(a4+a3).
因为d≠0,所以
| a | 4 |
| a | 3 |
又由S7=7得7a1+
| 7×6 |
| 2 |
联立①②解得a1=-5,d=2,
所以an=2n-7(n∈N*).
(2)由(1)知,当n≤3时,an<0;
当n>3时,an>0.
Sn=
| n(a1+an) |
| 2 |
| n(-5+2n-7) |
| 2 |
∴当n≤3时,Tn=-Sn=-n2+6n;
当n>3时,Tn=-S3+(Sn-S3)=Sn-2S3=(n2-6n)-2×(-9)=n2-6n+18.
综上,Tn=
|
(3)
| amam+1 |
| am+2 |
| (2m-7)(2m-5) |
| 2m-3 |
令2m-3=t,则
| amam+1 |
| am+2 |
| (t-4)(t-2) |
| t |
| 8 |
| t |
故t为8的约数,又∵t是奇数,∴t的可能取值为±1.
当t=1时,m=2,
| a2a3 |
| a4 |
当t=-1时,m=1,
| a1a2 |
| a3 |
所以满足条件的正整数m=2.
点评:本题考查数列的通项公式的求法,考查数列的绝对值的前n项和的求法,考查满足条件的实数的求法,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
如图所示,程序框图(算法流程图)的输出结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)=x3-4,则零点一定在( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(5,6) |
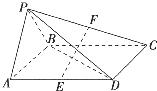 四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=
四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=