题目内容
已知0<x≤
,求函数f(x)=
的最值.
| 1 |
| 4 |
| x2-2x+2 |
| x |
考点:函数的最值及其几何意义
专题:计算题,导数的概念及应用
分析:利用导数,确定函数的单调性,即可求出函数的最值.
解答:
解:f(x)=
=x+
-2,
∵f′(x)=1-
,
∴0<x≤
时,f′(x)<0,
∴0<x≤
时,函数单调递减,
∴x=
时,函数有最小值
,无最大值.
| x2-2x+2 |
| x |
| 2 |
| x |
∵f′(x)=1-
| 2 |
| x2 |
∴0<x≤
| 1 |
| 4 |
∴0<x≤
| 1 |
| 4 |
∴x=
| 1 |
| 4 |
| 25 |
| 4 |
点评:本题考查函数的最值,考查导数知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
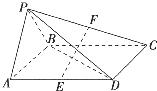 四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=
四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=