题目内容
某专营店经销某商品,当售价不高于10元时,每天能销售100件,当价格高于10元时,每提高1元,销量减少3件,若该专营店每日费用支出为500元,用x表示该商品定价,y表示该专营店一天的净收入(除去每日的费用支出后的收入).
(1)把y表示成x的函数;
(2)试确定该商品定价为多少元时,一天的净收入最高?并求出净收入的最大值.
(1)把y表示成x的函数;
(2)试确定该商品定价为多少元时,一天的净收入最高?并求出净收入的最大值.
考点:函数模型的选择与应用
专题:函数的性质及应用
分析:(1)根据条件建立分段函数关系即可;
(2)结合一元二次函数的最值性质即可求出函数的最值.
(2)结合一元二次函数的最值性质即可求出函数的最值.
解答:
(1)当0≤x≤10,y=100x-500,
当x>10,销量为100-3(x-10)=-3x+130,此时y=(-3x+130)x-500=-3x2+130x-500,
故y=
.
(2)当0≤x≤10,y=100x-500≤500,
当x>10,y=-3x2+130x-500=-3(x-
)2+(
)2-500,
∵x∈N,
∴当x=22时,函数取得最大值,此时y=-3×222+130×22-500=908,
综上当商品定价为22元时,一天的净收入最高,净收入的最大值为908.
当x>10,销量为100-3(x-10)=-3x+130,此时y=(-3x+130)x-500=-3x2+130x-500,
故y=
|
(2)当0≤x≤10,y=100x-500≤500,
当x>10,y=-3x2+130x-500=-3(x-
| 65 |
| 3 |
| 65 |
| 3 |
∵x∈N,
∴当x=22时,函数取得最大值,此时y=-3×222+130×22-500=908,
综上当商品定价为22元时,一天的净收入最高,净收入的最大值为908.
点评:本题主要考查函数应用问题,根据条件建立函数关系,利用一元二次函数的性质求最值是解决本题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知函数f(x)=
-lnx,则有下列结论中错误的是( )
| lnx |
| 1+x |
| A、?x0∈R,f(x)=0 | ||
| B、若x0是f(x)的最大值点,则f(x0)=x0 | ||
C、若x0是f(x)的最大值点,则f(x0)<
| ||
| D、若x0是f(x)的极大值点,则f(x)在(x0,+∞)上单调递增 |
设函数f(x)=
若f(f(t))≤2,则实数t的取值范围是( )
|
A、(-∞,
| ||
B、[
| ||
| C、(-∞,-2] | ||
| D、[-2,+∞) |
已知点P(3,m)在直线x+y-1=0上,则m的值为( )
| A、5 | B、2 | C、-2 | D、-6 |
已知直线l1:2x-y+1=0,l2:x-3y-=0,则l1到l2的角是( )
| A、45° | B、60° |
| C、120° | D、135° |
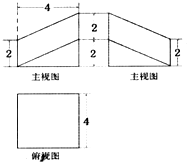 棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是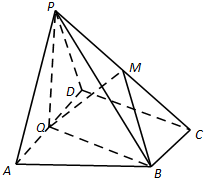 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=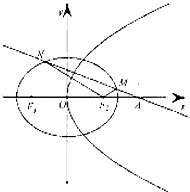 如图,己知椭圆C:
如图,己知椭圆C: