题目内容
椭圆
+
=1(a>b>0),点A为其上任意一点,左右焦点为F1,F2,若|AF1|,|F1F2|,|AF2|成等差数列,则此椭圆的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件,推导出2|F1F2|=|AF1|+|AF2|,由此利用椭圆的定义和性质能求出它的离心率.
解答:
解:椭圆
+
=1(a>b>0),点A为其上任意一点,
左右焦点为F1,F2,|AF1|,|F1F2|,|AF2|成等差数列,
∴2|F1F2|=|AF1|+|AF2|,
∴4c=2a,即a=2c,
∴e=
=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
左右焦点为F1,F2,|AF1|,|F1F2|,|AF2|成等差数列,
∴2|F1F2|=|AF1|+|AF2|,
∴4c=2a,即a=2c,
∴e=
| c |
| a |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查椭圆的离心率的求法,是基础题,解题时要注意等差数列的性质的合理运用.

练习册系列答案
相关题目
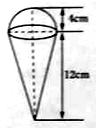 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π≈3.14)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π≈3.14)
 一正棱柱其三视图如图所示,该正多面体的体积为
一正棱柱其三视图如图所示,该正多面体的体积为