题目内容
求证:当x∈R时,任意f(x)都可以写成一个奇函数与一个偶函数的和.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先假设f(x)=g(x)+h(x)是存在的,再根据函数的奇偶性构造方程组,求出g(x)和h(x)的解析式,再由奇(偶)进行验证即可.
解答:
证明:设g(x)是R上的奇函数,h(x)是R上的偶函数,
先假设f(x)=g(x)+h(x)是存在的,则f(-x)=g(-x)+h(-x),
∵奇函数性质:g(x)=-g(-x),
偶函数性质:h(x)=h(-x)
∴
,
解得g(x)=
,h(x)=
,
则验证得,g(x)为R上的奇函数,h(x)为R上的偶函数,
由此我们得出结论,当x∈R时,对任意的f(x),我们能够构造这么两个函数
g(x)=
是奇函数,h(x)=
是偶函数,且f(x)=g(x)+h(x).
先假设f(x)=g(x)+h(x)是存在的,则f(-x)=g(-x)+h(-x),
∵奇函数性质:g(x)=-g(-x),
偶函数性质:h(x)=h(-x)
∴
|
解得g(x)=
| f(x)-f(-x) |
| 2 |
| f(x)+f(-x) |
| 2 |
则验证得,g(x)为R上的奇函数,h(x)为R上的偶函数,
由此我们得出结论,当x∈R时,对任意的f(x),我们能够构造这么两个函数
g(x)=
| f(x)-f(-x) |
| 2 |
| f(x)+f(-x) |
| 2 |
点评:本题是探究性的证明题,考查了函数奇偶性的定义及性质的应用,以及方程思想.

练习册系列答案
相关题目
(x-1)10的展开式中第6项系的系数是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
 执行如图所示的程序框图所表示的程序,则所得的结果为
执行如图所示的程序框图所表示的程序,则所得的结果为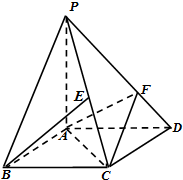 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD. 某办公室共有6人,组织出门旅行,旅行车上的6个座位如图所示,其中甲、乙两人的关系较为亲密,要求在同一排且相邻,则不同的安排方法有
某办公室共有6人,组织出门旅行,旅行车上的6个座位如图所示,其中甲、乙两人的关系较为亲密,要求在同一排且相邻,则不同的安排方法有 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).