题目内容
设摩天轮逆时针方向匀速旋转，24分钟旋转一周，轮上观光箱所在圆的方程为x2+y2=1．已知时间t=0时，观光箱A的坐标为（
，
），则当0≤t≤24时（单位：分），动点A的纵坐标y关于t的函数的单调递减区间是 ．
| 1 |
| 2 |
| ||
| 2 |
考点：函数解析式的求解及常用方法
专题：应用题,函数的性质及应用
分析：点A的初始角为
，结合图形知，当点A转到点B到点C时，动点A的纵坐标y关于t的函数的单调递减，再把角度区间转化为对应的时间区间即可．
| π |
| 3 |
解答：
解：t=0时，点A的坐标是 （
，
），
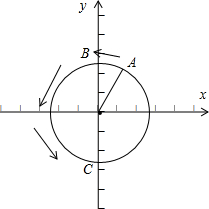
∴点A的初始角为
，如图所示；
当点A转到点B时，
动点A的纵坐标y关于t（单位：秒）的函数是减函数，到点C结束；
∵24分钟旋转一周，
∴每分钟转过的角度是
=
，∠AOB=
，∠BOC=π；
∴当2≤t≤14时，动点A的纵坐标y关于t（单位：秒）的函数单调递减．
故答案为：[2，14]．
| 1 |
| 2 |
| ||
| 2 |
∴点A的初始角为
| π |
| 3 |
当点A转到点B时，
动点A的纵坐标y关于t（单位：秒）的函数是减函数，到点C结束；
∵24分钟旋转一周，
∴每分钟转过的角度是
| 2π |
| 24 |
| π |
| 12 |
| π |
| 6 |
∴当2≤t≤14时，动点A的纵坐标y关于t（单位：秒）的函数单调递减．
故答案为：[2，14]．
点评：本题考查了求函数的单调性及单调区间的问题，解题时应根据题意，结合图形，得出所求问题的答案．是数形结合的应用题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设椭圆Γ1的中心和抛物线Γ2的顶点均为原点O，Γ1、Γ2的焦点均在x轴上，过Γ2的焦点F作直线l，与Γ2交于A、B两点，在Γ1、Γ2上各取两个点，将其坐标记录于下表中：