题目内容
在以下四个结论中:
①f(x)=3x是奇函数;
②g(x)=
是奇函数;
③F(x)=f(x)f(-x)(x∈R)是偶函数;
④h(x)=3x是非奇非偶函数.
正确的有( )个.
①f(x)=3x是奇函数;
②g(x)=
| ||
| |x+2|-2 |
③F(x)=f(x)f(-x)(x∈R)是偶函数;
④h(x)=3x是非奇非偶函数.
正确的有( )个.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:运用函数的奇偶性的定义,加以判断,注意定义域是否关于原点对称和函数的化简.
解答:
解:对于①,f(x)=3x是奇函数,故①对;
对于②,由1-x2≥0且|x+2|-2≠0,解得-1≤x≤1且x≠0,
则定义域关于原点对称,g(x)=
,g(-x)=-g(x),则为奇函数,故②对;
对于③,F(-x)=f(-x)f(x)=F(x),则为偶函数,故③对;
对于④,h(x)=3x是非奇非偶函数,故④对.
故选D.
对于②,由1-x2≥0且|x+2|-2≠0,解得-1≤x≤1且x≠0,
则定义域关于原点对称,g(x)=
| ||
| x |
对于③,F(-x)=f(-x)f(x)=F(x),则为偶函数,故③对;
对于④,h(x)=3x是非奇非偶函数,故④对.
故选D.
点评:本题考查函数的奇偶性的判断,注意定义域,以及函数的化简,运用定义法解题,属于基础题和易错题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知数列{an}的前S项和为Sn,且Sn=n-n2,则a4=( )
| A、-6 | B、-8 |
| C、-12 | D、-14 |
若a,b均为正实数,且
+
=1,则a+b的最小值是( )
| 4 |
| a |
| 3 |
| b |
A、6+2
| ||
B、7+2
| ||
C、6+4
| ||
D、7+4
|
已知函数f(x)=
,则f(2-log
3)=( )
|
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
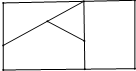 如图,用6种不同的颜色为一块广告牌着色,要求在四个区域中相邻的区域不用同一种颜色,则共有
如图,用6种不同的颜色为一块广告牌着色,要求在四个区域中相邻的区域不用同一种颜色,则共有