题目内容
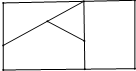如图，用6种不同的颜色为一块广告牌着色，要求在四个区域中相邻的区域不用同一种颜色，则共有考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：根据题意，分分四个步骤来完成着色，即依次考虑为①、②、③、④着色时各自的方法数，由乘法原理计算可得答案．
解答：
解：完成着色这件事，共分四个步骤，即依次考虑为①、②、③、④着色时各自的方法数，
为①着色有6种方法，
为②着色有5种方法，
为③着色有4种方法，
为④着色也只有4种方法．
∴共有着色方法6×5×4×4=480，
故答案为：480．
解：完成着色这件事，共分四个步骤，即依次考虑为①、②、③、④着色时各自的方法数，为①着色有6种方法，
为②着色有5种方法，
为③着色有4种方法，
为④着色也只有4种方法．
∴共有着色方法6×5×4×4=480，
故答案为：480．
点评：本题考查涂色问题，是排列、组合的典型题目，一般涉及分类加法原理与分步乘法原理，注意认真分析题意，把握好限制条件．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若a＞b＞0，则下列不等式不成立的是（ ）
A、
| ||||
| B、|a|＞|b| | ||||
C、
| ||||
| D、a3＞b3 |
在以下四个结论中：
①f（x）=3x是奇函数；
②g（x）=
是奇函数；
③F（x）=f（x）f（-x）（x∈R）是偶函数；
④h（x）=3x是非奇非偶函数．
正确的有（ ）个．
①f（x）=3x是奇函数；
②g（x）=
| ||
| |x+2|-2 |
③F（x）=f（x）f（-x）（x∈R）是偶函数；
④h（x）=3x是非奇非偶函数．
正确的有（ ）个．
| A、1个 | B、2个 | C、3个 | D、4个 |
下列函数中，与y=-3|x|的奇偶性相同，且在（-∞，0）上单调性也相同的是（ ）
A、y=-
| ||
B、y=|x|-
| ||
| C、y=-（2x+2-x） | ||
| D、y=x3-1 |
若函数f（x）=loga（x2+
x），（a＞0，a≠1）在区间（
，+∞）内恒有f（x）＜0，则f（x）的单调递减区间是（ ）
| 3 |
| 2 |
| 1 |
| 2 |
A、（-∞，-
| ||
B、（-∞，-
| ||
C、（-
| ||
| D、（0，+∞） |