题目内容
已知指数函数g(x)=ax满足:g(-3)=
,定义域为R的函数f(x)=
是奇函数.
(1)求f(x)的解析式;
(2)判断f(x)在其定义域上的单调性,并求函数的值域;
(3)若不等式:t•f(x)≥4x-2x+2+3对x∈[1,2]恒成立,求实数t的取值范围.
| 1 |
| 8 |
| g(x)-1 |
| g(x)+m |
(1)求f(x)的解析式;
(2)判断f(x)在其定义域上的单调性,并求函数的值域;
(3)若不等式:t•f(x)≥4x-2x+2+3对x∈[1,2]恒成立,求实数t的取值范围.
考点:函数恒成立问题,函数解析式的求解及常用方法,函数单调性的判断与证明,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)直接由g(-3)=
,求得a的值,得到g(x)的解析式,则f(x)可求,利用函数奇偶性的定义证明f(x)为奇函数;
(2)∵2x是定义域上的增函数,∴-
是定义域上的减函数,从而得到函数f(x)的单调性,由指数函数的值域求得f(x)的值域;
(3)把f(x)的解析式代入t•f(x)≥4x-2x+2+3,分离变量t后利用配方法求得(2x)2-2•2x-3在[1,2]
上的值域,从而求得实数t的取值范围.
| 1 |
| 8 |
(2)∵2x是定义域上的增函数,∴-
| 2 |
| 2x+1 |
(3)把f(x)的解析式代入t•f(x)≥4x-2x+2+3,分离变量t后利用配方法求得(2x)2-2•2x-3在[1,2]
上的值域,从而求得实数t的取值范围.
解答:
解:(1)∵g(x)=ax,
由g(-3)=
⇒a-3=
⇒a=2,∴f(x)=
,
又f(x)为奇函数,∴f(-x)=-f(x),即
=-
,
化简得1+m•2x=2x+m对x∈R恒成立,∴m=1,
故f(x)=
;
(2)f(x)=1-
,其定义域为R,
由2x为增函数可知f(x)是R上的增函数,
∵2x+1>1,∴0<
<1,-2<
<0,∴-1<f(x)<1,
即函数f(x)的值域为(-1,1);
(3)t•f(x)≥4x-2x+2+3对x∈[1,2]恒成立,
等价于t≥(2x)2-2•2x-3对x∈[1,2]恒成立,
而在[1,2]上(2x)2-2•2x-3=(2x-1)2-4的最大值为5.
故t≥5.
由g(-3)=
| 1 |
| 8 |
| 1 |
| 8 |
| 2x-1 |
| 2x+m |
又f(x)为奇函数,∴f(-x)=-f(x),即
| 2-x-1 |
| 2-x+m |
| 2x-1 |
| 2x+m |
化简得1+m•2x=2x+m对x∈R恒成立,∴m=1,
故f(x)=
| 2x-1 |
| 2x+1 |
(2)f(x)=1-
| 2 |
| 2x+1 |
由2x为增函数可知f(x)是R上的增函数,
∵2x+1>1,∴0<
| 1 |
| 2x+1 |
| -2 |
| 2x+1 |
即函数f(x)的值域为(-1,1);
(3)t•f(x)≥4x-2x+2+3对x∈[1,2]恒成立,
等价于t≥(2x)2-2•2x-3对x∈[1,2]恒成立,
而在[1,2]上(2x)2-2•2x-3=(2x-1)2-4的最大值为5.
故t≥5.
点评:本题考查指数函数性质,训练了函数奇偶性的判断方法,考查了复合函数单调性的判断方法,考查了恒成立问题,解决含有字母参数的恒成立问题,关键在于转化,即转化为求函数最值问题,然后利用配方法或借助于函数的单调性求解,是中档题.

练习册系列答案
相关题目
已知集合A={x|-2≤x≤2},B={x|0<x<1},则有( )
| A、A>B | B、A?B |
| C、B?A | D、A⊆B |
把6个人平均分成两组,再从各组中分别选出正组长1名和副组长1名,则不同的选法种数是( )
| A、720 | B、360 |
| C、120 | D、60 |
 如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=
如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD= 如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.
如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.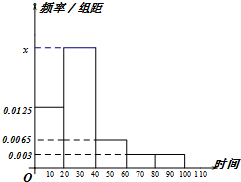 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].