题目内容

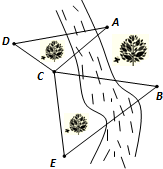如图，为了测量河对岸A、B两点之间的距离，观察者找到一个点C，从C点可以观察到点A、B；找到一个点D，从D点可以观察到点A、C；找到一个点E，从E点可以观察到点B、C；并测量得到一些数据：CD=2，CE=2
3
，∠D=45°，∠ACD=105°，∠ACB=48.19°，∠BCE=75°，∠E=60°，则A、B两点之间的距离为
 
．（其中cos48.19°取近似值
2
3
）
考点：解三角形的实际应用
专题：应用题,解三角形
分析：求出AC，通过正弦定理求出BC，然后利用余弦定理求出AB．
解答： 解：依题意知，在△ACD中，∠A=30°由正弦定理得AC=
CDsin45°
sin30°
=2
2

在△BCE中，∠CBE=45°，由正弦定理得BC=
CEsin60°
sin45°
=3
2

在△ABC中，由余弦定理AB2=AC2+BC2-2AC•BCcos∠ACB=10
∴AB=
10
．
故答案为：
10
．
点评：本题考查三角形的面积的求法，正弦定理与余弦定理的应用，考查计算能力．
练习册系列答案
相关题目
（1）若数列{an}是等差数列，对于bn=（
1
n
）（a1+a2+…+an），则数列{bn}也是等差数列，类比上述性质，若{cn}是各项为正数的等比数列，则数列{dn}（d＞0）也是等比数列，写出dn的表达式，并且证明你类比得到的命题是否为真命题．（2）设x＞0，y＞0，证明不等式（x2+y2） 
1
2
＞（x3+y3） 
1
3
．
对于四个正数x，y，z，w，如果xw＜yz，那么称（x，y）是（z，w）的“下位序对”．
（1）对于2，3，7，11，试求（2，7）的“下位序对”；
（2）设a，b，c，d均为正数，且（a，b）是（c，d）的“下位序对”，试判断
c
d
，
a
b
，
a+c
b+d
之间的大小关系；
（3）设正整数n满足条件：对集合{t|0＜t＜2014}内的每个m∈N+，总存在k∈N+，使得（m，2014）是（k，n）的“下位序对”，且（k，n）是（m+1，2015）的“下位序对”．求正整数n的最小值．
已知椭圆
x2
a2
+
y2
b2
=1(a＞0，b＞0）的右顶点为A，点M在椭圆上，且它的横坐标为1，点B（0，
3
），且
AB
=2
AM
．
（1）求椭圆的方程；
（2）若过点A的直线l与椭圆交于另一点N，若线段AN的垂直平分线经过点（
6
13
，0），求直线l的方程．
已知一个正方体的八个顶点都在一个球的表面上，若此正方体的棱长为2，那么这个球的表面积是
 
．注：S球=4πR2（R为球的半径）
已知直线y=
3
3
x与圆心在x轴正半轴，半径为2的圆C交于A、B两点，且|AB|=2
3
．
（1）已知点P（-1，
7
），Q是圆C上任意一点，求|PQ|的最大值；
（2）若过圆心任意作一条射线与圆C交于M点，求点M在劣弧
AB
上的概率．
直线l过椭圆C：
x2
2
+y2=1的左焦点F，且与椭圆C交于P，Q两点，M为弦PQ的中点，O为原点，若△PMO是以线段OF为底边的等腰三角形，则直线l的斜率为
 
．
已知函数f（x）=ax2+4x-3在区间[0，2]上的最小值为-4，求a的值．
已知函数f（x）=sin（ωx+
π
4
）（ω＞0）的最小正周期为π，则f（
π
8
）=（　　）
A、1
B、
1
2
C、-1
D、-
1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网