题目内容
已知函数f(x)=ax2+4x-3在区间[0,2]上的最小值为-4,求a的值.
考点:二次函数的性质
专题:函数的性质及应用
分析:分别讨论a的取值,结合一元二次函数的图象和性质即可得到结论.
解答:
解:1)当a=0时,f(x)=4x-3,f(x)min=f(0)=-3,不合题意;
2)当a>0时,对称轴x=-
=-
<0,函数在[0,2]上单调递增,f(x)min=-3,不合题意;(5分)
3)当a<0时,对称轴x=-
=-
>0,(6分)
当0<-
≤1时,函数在[0,-
]上递增,在[-
,2]上递减,f(x)min=f(2)=-4,
即4a+8-3=-4,解得a=-
(7分)
当1<-
≤2时,函数在[0,-
]上递增,在[-
,2]上递减,
f(x)min=f(0)=-3,不合题意;(8分)
当-
>2时,函数在[0,2]上递增,f(x)min=f(0)=-3 (9分)
综上所述,a=-
(10分)
2)当a>0时,对称轴x=-
| 4 |
| 2a |
| 2 |
| a |
3)当a<0时,对称轴x=-
| 4 |
| 2a |
| 2 |
| a |
当0<-
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
即4a+8-3=-4,解得a=-
| 9 |
| 4 |
当1<-
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
f(x)min=f(0)=-3,不合题意;(8分)
当-
| 2 |
| a |
综上所述,a=-
| 9 |
| 4 |
点评:本题主要考查一元二次函数的图象和性质,要对a进行分类讨论.

练习册系列答案
相关题目
直线4x+3y-5=0与圆(x-1)2+(y-2)2=9相交于A、B两点,则AB的长度等于( )
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|
已知两直线l1:3x+4y-2=0与l2:ax-8y-3=0平行,则a的值是( )
| A、3 | B、4 | C、6 | D、-6 |
若复数z满足z(1-i)=2,则复数z的共轭复数
=( )
. |
| z |
| A、1+i | ||||
| B、1-i | ||||
C、
| ||||
| D、2-2i |
在四边形ABCD中,若
=
+
,则四边形ABCD一定是( )
| AC |
| AB |
| AD |
| A、正方形 | B、菱形 |
| C、矩形 | D、平行四边形 |
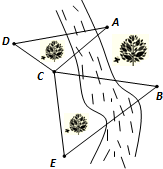 如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2
如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2