题目内容
已知直线y=
x与圆心在x轴正半轴,半径为2的圆C交于A、B两点,且|AB|=2
.
(1)已知点P(-1,
),Q是圆C上任意一点,求|PQ|的最大值;
(2)若过圆心任意作一条射线与圆C交于M点,求点M在劣弧
上的概率.
| ||
| 3 |
| 3 |
(1)已知点P(-1,
| 7 |
(2)若过圆心任意作一条射线与圆C交于M点,求点M在劣弧
 |
| AB |
考点:几何概型,直线和圆的方程的应用
专题:直线与圆,概率与统计
分析:(Ⅰ)由题意,圆心到直线的距离为1,利用点到直线的距离公式,建立方程,即可求圆C的方程;
解答:
解:(1)由题意,半径为2的圆C交于A、B两点,且|AB|=2
.
得到圆心到直线的距离为1,
设圆心为(a,0)(a>0),则
=1,
∴a=2,
∴圆C的方程为(x-2)2+y2=4;
点P(-1,
)在圆外,Q是圆C上任意一点,所以|PQ|的最大值为PC+r=
+2=6;
(2)由(1)可得∠AOB=120°,所以过圆心任意作一条射线与圆C交于M点,点M在劣弧
上的概率为
=
.
| 3 |
得到圆心到直线的距离为1,
设圆心为(a,0)(a>0),则
|
| ||
|
∴a=2,
∴圆C的方程为(x-2)2+y2=4;
点P(-1,
| 7 |
(-1-2)2+(
|
(2)由(1)可得∠AOB=120°,所以过圆心任意作一条射线与圆C交于M点,点M在劣弧
 |
| AB |
| 120° |
| 360° |
| 1 |
| 3 |
点评:本题考查了直线与圆的位置关系、点到直线的距离、几何概型的概率等知识点,属于中档题.

练习册系列答案
相关题目
已知点A(3,a)在直线2x+y-7=0上,则a=( )
| A、1 | B、-1 | C、2 | D、-2 |
在△ABC中,
•
=
•
,则△ABC一定是( )
| AB |
| BC |
| AC |
| CB |
| A、等腰三角形 |
| B、锐角三角形 |
| C、直角三角形 |
| D、钝角三角形 |
已知两直线l1:3x+4y-2=0与l2:ax-8y-3=0平行,则a的值是( )
| A、3 | B、4 | C、6 | D、-6 |
若复数z满足z(1-i)=2,则复数z的共轭复数
=( )
. |
| z |
| A、1+i | ||||
| B、1-i | ||||
C、
| ||||
| D、2-2i |
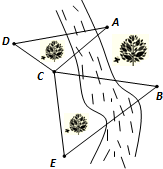 如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2
如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2