题目内容
对于四个正数x,y,z,w,如果xw<yz,那么称(x,y)是(z,w)的“下位序对”.
(1)对于2,3,7,11,试求(2,7)的“下位序对”;
(2)设a,b,c,d均为正数,且(a,b)是(c,d)的“下位序对”,试判断
,
,
之间的大小关系;
(3)设正整数n满足条件:对集合{t|0<t<2014}内的每个m∈N+,总存在k∈N+,使得(m,2014)是(k,n)的“下位序对”,且(k,n)是(m+1,2015)的“下位序对”.求正整数n的最小值.
(1)对于2,3,7,11,试求(2,7)的“下位序对”;
(2)设a,b,c,d均为正数,且(a,b)是(c,d)的“下位序对”,试判断
| c |
| d |
| a |
| b |
| a+c |
| b+d |
(3)设正整数n满足条件:对集合{t|0<t<2014}内的每个m∈N+,总存在k∈N+,使得(m,2014)是(k,n)的“下位序对”,且(k,n)是(m+1,2015)的“下位序对”.求正整数n的最小值.
考点:不等式的基本性质
专题:不等式
分析:(1)据新定义,代入计算判断即可;
(2)根据新定义得到ad<bc,再利用不等式的性质,即可判断;
(3)由题意得到
,继而求出n≥4029,再验证该式对集合{t|0<t<2014}内的每个m∈N+的每个正整数m都成立,继而求出最小值
(2)根据新定义得到ad<bc,再利用不等式的性质,即可判断;
(3)由题意得到
|
解答:
解:(1)∵3×7<11×2,
∴(2,7)的下位序对是(3,11).
(2)∵(a,b)是(c,d)的“下位序对”,
∴ad<bc,
∵a,b,c,d均为正数,故
-
=
>0,即
-
>0,所以
>
;
同理
<
.
综上所述,
<
<
.
(3)依题意,得
,
注意到m,n,l整数,故
,
于是2014(mn+n-1)≥2014×2015k≥2015(mn+1),
∴n≥
,
该式对集合{t|0<t<2014}内的每个m∈N+的每个正整数m都成立
∴n≥
=4029,
∵
<
<
,
∴
<
<
,
∴
<
<
,
∴对集合{t|0<t<2014}内的每个m∈N+,总存在k∈N+,使得(m,2014)是(k,n)的“下位序对”,且(k,n)是(m+1,2015)的“下位序对”.
正整数n的最小值为4029
∴(2,7)的下位序对是(3,11).
(2)∵(a,b)是(c,d)的“下位序对”,
∴ad<bc,
∵a,b,c,d均为正数,故
| a+c |
| b+d |
| a |
| b |
| bc-ad |
| (b+d)b |
| a+c |
| b+d |
| a |
| b |
| a+c |
| b+d |
| a |
| b |
同理
| a+c |
| b+d |
| c |
| d |
综上所述,
| a |
| b |
| a+c |
| b+d |
| c |
| d |
(3)依题意,得
|
注意到m,n,l整数,故
|
于是2014(mn+n-1)≥2014×2015k≥2015(mn+1),
∴n≥
| 4029 |
| 2014-m |
该式对集合{t|0<t<2014}内的每个m∈N+的每个正整数m都成立
∴n≥
| 4029 |
| 2014-2013 |
∵
| m |
| 2014 |
| k |
| n |
| m+1 |
| 2015 |
∴
| m |
| 2014 |
| m+m+1 |
| 2014+2015 |
| m+1 |
| 2015 |
∴
| m |
| 2014 |
| 2m+1 |
| 4029 |
| m+1 |
| 2015 |
∴对集合{t|0<t<2014}内的每个m∈N+,总存在k∈N+,使得(m,2014)是(k,n)的“下位序对”,且(k,n)是(m+1,2015)的“下位序对”.
正整数n的最小值为4029
点评:本题考查了新定义的学习和利用,关键掌握读懂新定义,属于难题

练习册系列答案
相关题目
某工厂某种产品的年固定成本为250万元,每生产x千件该产品需另投入成本为G(x),当年产量不足80千件时,G(x)=
x2+10x(万元);当年产量不小于80千件时,G(x)=51x+
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完,则该厂在这一商品的生产中所获年利润的最大值是( )
| 1 |
| 3 |
| 10000 |
| x |
| A、1150万元 |
| B、1000万元 |
| C、950万元 |
| D、900万元 |
直线4x+3y-5=0与圆(x-1)2+(y-2)2=9相交于A、B两点,则AB的长度等于( )
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|

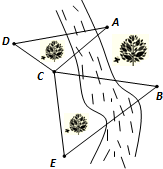 如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2
如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2