题目内容
已知一个正方体的八个顶点都在一个球的表面上,若此正方体的棱长为2,那么这个球的表面积是 .注:S球=4πR2(R为球的半径)
考点:球的体积和表面积
专题:计算题,空间位置关系与距离,球
分析:设正方体的外接球的半径为r,由正方体的对角线长即为球的直径,再与球的表面积公式,计算即可得到.
解答:
解:设正方体的外接球的半径为R,
由正方体的对角线长即为球的直径,
则2
=2r,
即R=
,
即有球的表面积为S=4πR2=4π×3=12π.
故答案为:12π.
由正方体的对角线长即为球的直径,
则2
| 3 |
即R=
| 3 |
即有球的表面积为S=4πR2=4π×3=12π.
故答案为:12π.
点评:本题考查正方体与外接球的位置关系,考查球的表面积公式的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
有10个乒乓球,将它们任意分成两堆,求出这两堆乒乓球个数的乘积,再将每堆乒乓球任意分成两堆并求出这两堆乒乓球个数的乘积,如此下去,直到不能再分为止,则所有乘积的和为( )
| A、45 | B、55 | C、90 | D、100 |
不等式
<1的解集是( )
| x |
| |x+1| |
| A、{x|-1<x<0} |
| B、{x|x∈R,且x≠-1} |
| C、R |
| D、{x|0<x,1} |

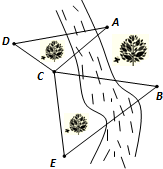 如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2
如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C;找到一个点E,从E点可以观察到点B、C;并测量得到一些数据:CD=2,CE=2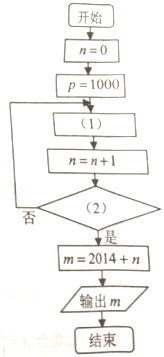 某电机厂2014年年底有资金1000万元,由于引进了先进生产设备,资金年平均增长率可达到50%,现在要设计一个程序,计算该电机厂的资金首次超过8000万元时,是哪一年的年底.
某电机厂2014年年底有资金1000万元,由于引进了先进生产设备,资金年平均增长率可达到50%,现在要设计一个程序,计算该电机厂的资金首次超过8000万元时,是哪一年的年底.