题目内容
已知数列{an}的前n项和Sn满足(t-1)Sn=t(an-2),(t为常数,t≠0且t≠1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=Sn-1,且数列{bn}为等比数列.
①求t的值;
②若cn=(-an)•log3(-bn),求数列{cn}的前n和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=Sn-1,且数列{bn}为等比数列.
①求t的值;
②若cn=(-an)•log3(-bn),求数列{cn}的前n和Tn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(I)利用“当n=1,a1=S1时,当n≥2时,an=Sn-Sn-1”及等比数列的通项公式即可得出;
(II)(Ⅱ)①数列{bn}为等比数列,可得
=b1b3,解得t=
.代入(t-1)Sn=t(an-2),即可得出bn=Sn-1.
②cn=(-an)•log3(-bn)=
,利用“错位相减法”及其等比数列的前n项和公式即可得出.
(II)(Ⅱ)①数列{bn}为等比数列,可得
| b | 2 2 |
| 1 |
| 3 |
②cn=(-an)•log3(-bn)=
| 2n |
| 3n |
解答:
解:(Ⅰ)由(t-1)Sn=t(an-2),(t-1)Sn+1=t(an+1-2),(t为常数,t≠0且t≠1).
作差得(t-1)an+1=t(an+1-an),化为an+1=tan,
当n=1时,(t-1)a1=t(a1-2),解得a1=2t.
即数列{an}成等比,an=a1•tn-1=2tn.
(Ⅱ)①∵数列{bn}为等比数列,
∴
=b1b3,
代入得(2t+2t2-1)2=(2t-1)(2t+2t2+2t3-1),
整理得6t3=2t2,t≠0.
解得t=
.
∴-
Sn=
(2×
-2),
∴Sn=1-
.
∴bn=Sn-1=-
,
数列{bn}为等比数列.
②cn=(-an)•log3(-bn)=
,
∴Tn=
+
+
+…+
,
Tn=
+
+…+
+
,
作差得
Tn=
+
+…+
-
=
-
=1-
,
故Tn=
-
.
作差得(t-1)an+1=t(an+1-an),化为an+1=tan,
当n=1时,(t-1)a1=t(a1-2),解得a1=2t.
即数列{an}成等比,an=a1•tn-1=2tn.
(Ⅱ)①∵数列{bn}为等比数列,
∴
| b | 2 2 |
代入得(2t+2t2-1)2=(2t-1)(2t+2t2+2t3-1),
整理得6t3=2t2,t≠0.
解得t=
| 1 |
| 3 |
∴-
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3n |
∴Sn=1-
| 1 |
| 3n |
∴bn=Sn-1=-
| 1 |
| 3n |
数列{bn}为等比数列.
②cn=(-an)•log3(-bn)=
| 2n |
| 3n |
∴Tn=
| 2 |
| 3 |
| 4 |
| 32 |
| 6 |
| 33 |
| 2n |
| 3n |
| 1 |
| 3 |
| 2 |
| 32 |
| 4 |
| 33 |
| 2(n-1) |
| 3n |
| 2n |
| 3n+1 |
作差得
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 3n |
| 2n |
| 3n+1 |
| ||||
1-
|
| 2n |
| 3n+1 |
| 2n+3 |
| 3n+1 |
故Tn=
| 3 |
| 2 |
| 2n+3 |
| 2•3n |
点评:本题考查了等比数列的定义、通项公式及前n项和公式、“错位相减法”,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知定义在R上的函数f(x)满足下列三个条件:
①对任意的x∈R,都有f(x+4)=f(x);
②对任意的0≤x1<x2≤2,都有f(x1)<f(x2);
③y=f(x+2)的图象关于y轴对称,
则下列结论中,正确的是( )
①对任意的x∈R,都有f(x+4)=f(x);
②对任意的0≤x1<x2≤2,都有f(x1)<f(x2);
③y=f(x+2)的图象关于y轴对称,
则下列结论中,正确的是( )
| A、f(7)<f(4.5)<f(6.5) |
| B、f(7)<f(6.5)<f(4.5) |
| C、f(4.5)<f(6.5)<f(7) |
| D、f(4.5)<f(7)<f(6.5) |
不等式x2-3x+2<0的解集是( )
| A、{x|x<-2或x>-1} |
| B、{x|x<1或x>2} |
| C、{x|1<x<2} |
| D、{x|-2<x-1} |
数列{
}的前n项和为Sn,且满足a1=1,an=an-1+n,(n≥2),则Sn等于( )
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
设全集为R,函数f(x)=
的定义域为M,函数f(x)=ln(x2-4x)的定义域为N,则M∩N=( )
| 4-x2 |
| A、[-2,0) |
| B、(-∞,-2] |
| C、(4,+∞) |
| D、(-∞,0]∪(4,+∞) |
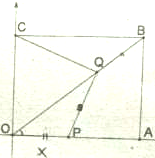 如图,在矩形OABC中,O为原点,B点坐标为(8,6).
如图,在矩形OABC中,O为原点,B点坐标为(8,6).