题目内容

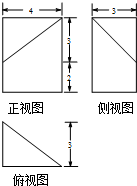
若某几何体的三视图如图所示，则此几何体的体积等于（　　）
A、4B、12C、24D、30
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据几何体的三视图得出该几何体是三棱柱去掉一个三棱锥所得的几何体，结合三视图的数据，求出它的体积．
解答： 解：根据几何体的三视图，得该几何体是三棱柱截去一个三棱锥后所剩几何体，
几何体是底面为边长为3，4，5的三角形，高为5的三棱柱被平面截得的，
如图所示，
所以该几何体的体积为：V三棱柱-V三棱锥=
1
2
×3×4×5-
1
3
×
1
2
×3×4×3=24．
故选：C．
点评：本题考查了利用空间几何体的三视图求几何体的体积的应用问题，解题的关键是由三视图得出几何体的结构特征是什么．
练习册系列答案
相关题目
如图所示的数阵叫“莱布尼兹调和三角形”，他们是由整数的倒数组成的，第n行有n个数且两端的数均为
1
n
(n≥2)，每个数是它下一行左右相邻两数的和，如：
1
1
=
1
2
+
1
2
，
1
2
=
1
3
+
1
6
，
1
3
=
1
4
+
1
12
…，则
（1）第6行第3个数字是
 
．
（2）第n（n≥3）行第3个数字是
 
．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左右焦点分别为F1，F2，过F1作圆：x2+y2=
a2
4
的切线，切点为E，延长F1E交双曲线右支于点P，若|OP|=
1
2
|F1F2|（O为坐标原点），则双曲线的离心率为
 
．
如图，已知PA⊥矩形ABCD所在的平面，E，F分别为AB，PC的中点，
（1）证明：EF∥平面PAD；
（2）若PA=AD，求证：EF⊥平面PCD．
半径为R的球O中有一内接圆柱．当圆柱的侧面积最大时，圆柱的侧面积与球的表面积之比是
 
．
一个几何体的三视图及其尺寸如图，则该几何体的表面积为（　　）
A、24πB、15π
C、15D、24
若不等式|x-3|+|x+5|-ax＞0（x∈R，a＞0）恒成立，则实数a的取值范围为
 
．
设曲线C的参数方程为
x=2+3cosθ
y=-1+3sinθ
(θ为参数)，直线l的极坐标方程为3ρcosθ+4ρsinθ+3=0，则曲线C上到直线l的距离为2的点有
 
个．
若A
 
2
n
＞6C
 
4
n
，则正整数n的取值集合为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网