题目内容
若M为RT△ABC斜边AB的中点，PM⊥平面ABC，则（ ）
| A、PA=PB=PC |
| B、PA=PB＞PC |
| C、PA=PB＜PC |
| D、PA≠PB |
考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：由直角三角形的性质得AM=BM=CM，再由射影性质得PA=PB=PC．
解答：
解：∵M为RT△ABC斜边AB的中点，
∴AM=BM=CM，
∵PM⊥平面ABC，
∴由射影定理得PA=PB=PC，
故选：A．
∴AM=BM=CM，
∵PM⊥平面ABC，
∴由射影定理得PA=PB=PC，
故选：A．
点评：本题考查三条线段长的大小的比较，是基础题，解题时要认真审题，注意直角三角形性质和射影定理的合理运用．
练习册系列答案
相关题目
若a，b，c是△ABC的三边，且
＞1，则△ABC一定是（ ）
| c | ||
|
| A、直角三角形 |
| B、等边三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
如图所示，四边形ABEF和ABCD都是直角梯形，∠BAD=∠FAB=90°，BC
如图所示的数阵叫“莱布尼兹调和三角形”，他们是由整数的倒数组成的，第n行有n个数且两端的数均为已知全集A={0，2，4，6}，集合B={2，4，5，6}，则A∩B等于（ ）
| A、{0，2，4，6，} |
| B、{2，4，6} |
| C、{0，2，4，5} |
| D、{0，5} |
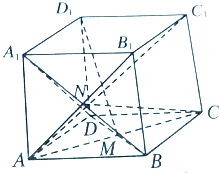如图，在正方形ABCD-A1B1C1D1中，M，N分别为正方形ABCD和AA1B1B的重心．