题目内容
5.已知f(x)是定义在R上的函数,图象关于y轴对称,且在x∈[0,+∞)单调递增.f(-2)=1,那么f(x)≤1的解集是( )
| A. | [-2,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,2) |
分析 根据函数奇偶性和单调性之间的关系,得出具体不等式,即可得出结论.
解答 解:∵函数y=f(x)的图象关于y轴对称,
∴f(x)是偶函数,则f(-2)=f(2),
∵函数f(x)在区间x∈[0,+∞)上为增函数,f(x)≤1,
∴|x|≤2,
∴-2≤x≤2,
故选A.
点评 本题主要考查不等式的解法,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
17.下列函数中,在(0,+∞)上为减函数的是( )
| A. | y=x+1 | B. | $y={log_{\frac{1}{2}}}x$ | C. | y=2x | D. | y=-(x-1)2 |
14.抛掷两枚质地的骰子,得到的点数分别为a,b,那么直线bx+ay=1的斜率$k≥-\frac{2}{5}$的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
 ,下列命题正确的是( )
,下列命题正确的是( ) , 则
, 则
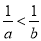
 ,则
,则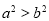
 ,则
,则