题目内容
18.已知函数f(x)=$\frac{{e}^{x}}{x}-kx$(e为自然对数的底数)有且只有一个零点,则实数k的取值范围是( )| A. | (0,2) | B. | (0,$\frac{{e}^{2}}{4}$) | C. | (0,e) | D. | (0,+∞) |
分析 求出函数的导函数,求出函数的最小值,根据函数的零点和最值关系即可得到结论.
解答 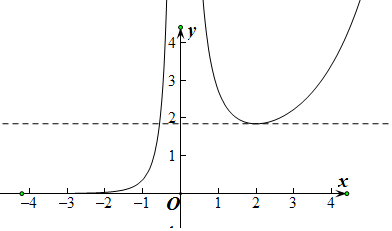 解:f(x)=0,即$\frac{{e}^{x}}{x}-kx$=0,
解:f(x)=0,即$\frac{{e}^{x}}{x}-kx$=0,
∵x≠0,
∴k=$\frac{{e}^{x}}{{x}^{2}}$,
令g(x)=$\frac{{e}^{x}}{{x}^{2}}$,
则g′(x)=$\frac{{e}^{x}(x-2)}{{x}^{3}}$,
令g′(x)=0,解得x=2,
当x>2或x<0时,g′(x)>0,函数g(x)单调递增,
当0<x<2时,g′(x)>0,函数g(x)单调递增,
∴当x=2时,函数有极小值,即g(2)=$\frac{{e}^{2}}{4}$,
且当x<0,时,f(x)∈(0,+∞),
∵函数f(x)=$\frac{{e}^{x}}{x}-kx$(e为自然对数的底数)有且只有一个零点,结合图象可得,
∴0<k<$\frac{{e}^{2}}{4}$,
故选:B
点评 本题考查的知识点是根的存在性及根的个数判断,其中熟练掌握函数零点与方程根之间的对应关系是解答的关键,利用导数是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.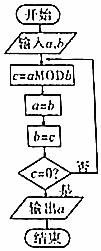 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )| A. | 0 | B. | 25 | C. | 50 | D. | 75 |
6.已知三个向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,且均为单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的取值范围是( )
| A. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | B. | [1,$\sqrt{2}$] | C. | [$\sqrt{2}$,$\sqrt{3}$] | D. | [$\sqrt{2}$-1,1] |
13.设sin(π-θ)=$\frac{1}{3}$,则cos2θ=( )
| A. | ±$\frac{4\sqrt{2}}{9}$ | B. | $\frac{7}{9}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | -$\frac{7}{9}$ |
3.函数y=$\frac{1+x}{1-x}$的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
10.“ln(x+2)<0”是“x<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |