题目内容
4．在区间[0，8]上随机取一个x的值，执行如图的程序框图，则输出的y≥3的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
分析 利用分段函数，求出输出的y≥3时，x的范围，以长度为测度求出相应的概率．
解答 解：由题意，0≤x≤6，2x-1≥3，∴2≤x≤6；
6＜x≤8，$\frac{x}{3}≥3$，无解，
∴输出的y≥3的概率为$\frac{6-2}{8-0}$=$\frac{1}{2}$，
故选B．
点评 本题考查程序框图，考查概率的计算，正确求出输出的y≥3时，x的范围是关键．
练习册系列答案
相关题目
14．已知向量$\overrightarrow{a}$=（2，-4），$\overrightarrow{b}$=（-3，x），$\overrightarrow{c}$=（1，-1），若（2$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{c}$，则|$\overrightarrow{b}$|=（ ）
| A． | 9 | B． | 3 | C． | $\sqrt{109}$ | D． | 3$\sqrt{10}$ |
12．抛物线y2=4x的焦点为F，点A（5，3），M为抛物线上一点，且M不在直线AF上，则△MAF周长的最小值为（ ）
| A． | 10 | B． | 11 | C． | 12 | D． | 6+$\sqrt{29}$ |
19．执行如图所示的程序框图，输出的x的值为（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
13．设sin（π-θ）=$\frac{1}{3}$，则cos2θ=（ ）
| A． | ±$\frac{4\sqrt{2}}{9}$ | B． | $\frac{7}{9}$ | C． | -$\frac{4\sqrt{2}}{9}$ | D． | -$\frac{7}{9}$ |
14．运行如图所示的算法框图，输出的结果是（ ）
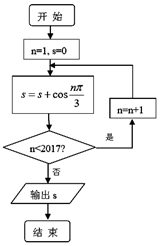
| A． | -1 | B． | 0 | C． | $\frac{1}{2}$ | D． | $-\frac{3}{2}$ |