题目内容
14.已知圆C的参数方程为$\left\{\begin{array}{l}{x=-1+cosα}\\{y=1+sinα}\end{array}\right.$ (α为参数),当圆心C到直线kx+y+4=0的距离最大时,k的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{5}$ |
分析 直线kx+y+4=0经过定点P(0,-4),当直线与PC垂直时,当圆心C到直线kx+y+4=0的距离最大,利用互相垂直的直线斜率直角的关系即可得出.
解答 解:圆C的参数方程为$\left\{\begin{array}{l}{x=-1+cosα}\\{y=1+sinα}\end{array}\right.$ (α为参数),化为:(x+1)2+(y-1)2=1,可得圆心C(-1,1).
直线kx+y+4=0经过定点P(0,-4),当直线与PC垂直时,当圆心C到直线kx+y+4=0的距离最大,∴$\frac{-4-1}{0-(-1)}•(-k)$=-1,
解得k=-$\frac{1}{5}$.
故选:D.
点评 本题考查了互相垂直的直线斜率直角的关系、直线经过定点问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.已知在△ABC中,a,b,c分别是∠BAC,∠ABC,∠ACB的对边,若过点C作垂直于AB的垂线CD,且CD=h,则下列给出的关于a,b,c,h的不等式中正确的是( )
| A. | a+b≥$\sqrt{2{h}^{2}+2{c}^{2}}$ | B. | a+b≥$\sqrt{4{h}^{2}+{c}^{2}}$ | C. | a+b≥$\sqrt{4{h}^{2}+2{c}^{2}}$ | D. | a+b≥$\sqrt{{h}^{2}+2{c}^{2}}$ |
9.观察下列各式:a1=1,a2=3,a3=4,a4=7,a5=11,…则a10=( )
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
6.设集合A={x|x>0},B={x|x2-5x-14<0},则A∩B等于( )
| A. | {x|0<x<5} | B. | {x|2<x<7} | C. | {x|2<x<5} | D. | {x|0<x<7} |
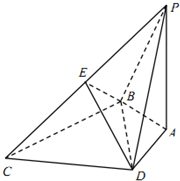 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.