题目内容
16.已知向量$\overrightarrow{m}$与向量$\overrightarrow{n}$平行,其中$\overrightarrow{m}$=(2,8),$\overrightarrow{n}$=(-4,t),则t=-16.分析 根据平面向量平行的坐标表示,列出方程求出t的值.
解答 解:$\overrightarrow{m}$∥$\overrightarrow{n}$,且$\overrightarrow{m}$=(2,8),$\overrightarrow{n}$=(-4,t),
∴2t-8×(-4)=0,
解得t=-16.
故答案为:-16.
点评 本题考查了平面向量平行的坐标表示与应用问题,是基础题目.

练习册系列答案
相关题目
4.设集合A={x|-1<x<1},B={x|log2x<-1},则A∩B=( )
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({-1,\frac{1}{2}})$ |
11. 如图,在△ABC中,∠ABC=90°,$AB=\sqrt{3}$,BC=1,P为△ABC内一点,∠BPC=90°,∠APB=120°,则tan∠PBA=$\frac{\sqrt{3}}{5}$.
如图,在△ABC中,∠ABC=90°,$AB=\sqrt{3}$,BC=1,P为△ABC内一点,∠BPC=90°,∠APB=120°,则tan∠PBA=$\frac{\sqrt{3}}{5}$.
 如图,在△ABC中,∠ABC=90°,$AB=\sqrt{3}$,BC=1,P为△ABC内一点,∠BPC=90°,∠APB=120°,则tan∠PBA=$\frac{\sqrt{3}}{5}$.
如图,在△ABC中,∠ABC=90°,$AB=\sqrt{3}$,BC=1,P为△ABC内一点,∠BPC=90°,∠APB=120°,则tan∠PBA=$\frac{\sqrt{3}}{5}$.
14.已知圆C的参数方程为$\left\{\begin{array}{l}{x=-1+cosα}\\{y=1+sinα}\end{array}\right.$ (α为参数),当圆心C到直线kx+y+4=0的距离最大时,k的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{5}$ |
15.已知集合A={x|x2-x-6<0},B={x|$\frac{x+4}{x-2}$>0},则A∩B等于( )
| A. | (-2,3) | B. | (2,3) | C. | (-4,-2) | D. | (-4,3) |
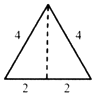
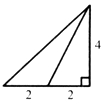
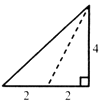
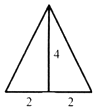
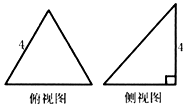 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )