题目内容
在△ABC中,内角A、B、C所对的边分别为a、b、c,a=2,且(2+b)(sinA-sinB)=c(sinC-sinB),则△ABC面积的最大值为 .
考点:正弦定理,余弦定理
专题:解三角形
分析:由条件利用正弦定理可得b2+c2-bc=4.再利用基本不等式可得bc≤4,当且仅当b=c=2时,取等号,此时,△ABC为等边三角形,从而求得它的面积
bcsinA的值.
| 1 |
| 2 |
解答:
解:△ABC中,∵a=2,且(2+b)(sinA-sinB)=c(sinC-sinB),
∴利用正弦定理可得(2+b)(a-b)=(c-b)c,即 b2+c2-bc=4.
再利用基本不等式可得 4≥2bc-bc=bc,∴bc≤4,当且仅当b=c=2时,取等号,
此时,△ABC为等边三角形,它的面积为
bcsinA=
×2×2×
=
,
故答案为:
.
∴利用正弦定理可得(2+b)(a-b)=(c-b)c,即 b2+c2-bc=4.
再利用基本不等式可得 4≥2bc-bc=bc,∴bc≤4,当且仅当b=c=2时,取等号,
此时,△ABC为等边三角形,它的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故答案为:
| 3 |
点评:本题主要考查正弦定理的应用,基本不等式,属于中档题.

练习册系列答案
相关题目
要得到函数y=2cos(2x-
)的图象,只要将函数y=2cos2x的图象( )
| π |
| 6 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
 已知函数f(x)=2sin(2ωx+
已知函数f(x)=2sin(2ωx+| π |
| 6 |
| π |
| 6 |
(1)试求ω的值;
(2)先列表,再作出函数f(x)在区间x∈[-π,π]上的图象.
定义域为R的函数f(x)满足f(x+2)=3f(x),当x∈[0,2)时,f(x)=
,若x∈[-4,-2)时,f(x)-
+
≥0恒成立,则实数t的取值范围是( )
|
| t |
| 9 |
| 2 |
| 9t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
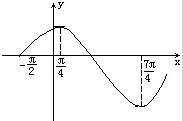 函数f(x)=sin(ωx+φ)(|φ|<
函数f(x)=sin(ωx+φ)(|φ|<