题目内容
数列{an}前n项和Sn,已知Sn=
an-
×3n+
,求和
+
+…+
<
.
| 9 |
| 8 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| S1 |
| 32 |
| S2 |
| 3n |
| Sn |
| 3 |
| 16 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:由已知得{
an+4×3n-2}是首项为4,公比为9的等比数列,从而an=
(9n-3n),进而Sn=4×9n-16×3n-1+
,由此得到
=
=
=
,当n≥2时,
=
<
•
<
×
,由此能证明
+
+…+
<
.
| 1 |
| 8 |
| 32 |
| 9 |
| 4 |
| 3 |
| 3n |
| Sn |
| 3n | ||
4×9n-16×3n-1+
|
| 1 | ||||
4×3n-
|
| 1 | ||||
|
| 3n |
| Sn |
| 1 | ||||
|
| 3 |
| 4 |
| 1 |
| 3n+1-4 |
| 3 |
| 8 |
| 1 |
| 3n |
| 3 |
| S1 |
| 32 |
| S2 |
| 3n |
| Sn |
| 3 |
| 16 |
解答:
解:∵Sn=
an-
×3n+
,①
∴Sn-1=
an-1-
×3n-1+
,②
①-②,得an=
an-
an-1-
×3n+
×3n-1,
整理,得
an+4×3n-2=
an-1+4×3n-1=9(
an-1+4×3n-3),
又a1=S1=
a1-
×3+
,解得a1=
,
a1+4×3-1=4,
∴{
an+4×3n-2}是首项为4,公比为9的等比数列,
∴
an+4×3n-2=4×9n-1,
∴an=
(9n-3n),
∴Sn=
[
-
]
=4(9n-1)-
(3n-1)
=4×9n-16×3n-1+
,
∴
=
=
=
,
当n=1时,
=
<
,
当n≥2时,3n+1-4>2×3n,
∴
=
<
•
<
×
,
∴
+
+…+
<
(
+
+…+
)
=
×
=
×
(1-
)
=
(1-
)<
.
综上所述,
+
+…+
<
.
| 9 |
| 8 |
| 4 |
| 3 |
| 4 |
| 3 |
∴Sn-1=
| 9 |
| 8 |
| 4 |
| 3 |
| 4 |
| 3 |
①-②,得an=
| 9 |
| 8 |
| 9 |
| 8 |
| 4 |
| 3 |
| 4 |
| 3 |
整理,得
| 1 |
| 8 |
| 9 |
| 8 |
| 1 |
| 8 |
又a1=S1=
| 9 |
| 8 |
| 4 |
| 3 |
| 4 |
| 3 |
| 64 |
| 3 |
| 1 |
| 8 |
∴{
| 1 |
| 8 |
∴
| 1 |
| 8 |
∴an=
| 32 |
| 9 |
∴Sn=
| 32 |
| 9 |
| 9(1-9n) |
| 1-9 |
| 3(1-3n) |
| 1-3 |
=4(9n-1)-
| 16 |
| 3 |
=4×9n-16×3n-1+
| 4 |
| 3 |
∴
| 3n |
| Sn |
| 3n | ||
4×9n-16×3n-1+
|
| 1 | ||||
4×3n-
|
| 1 | ||||
|
当n=1时,
| 3 |
| S1 |
| 9 |
| 64 |
| 3 |
| 16 |
当n≥2时,3n+1-4>2×3n,
∴
| 3n |
| Sn |
| 1 | ||||
|
| 3 |
| 4 |
| 1 |
| 3n+1-4 |
| 3 |
| 8 |
| 1 |
| 3n |
∴
| 3 |
| S1 |
| 32 |
| S2 |
| 3n |
| Sn |
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
=
| 3 |
| 8 |
| ||||
1-
|
=
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 3n |
=
| 3 |
| 16 |
| 1 |
| 3n |
| 3 |
| 16 |
综上所述,
| 3 |
| S1 |
| 32 |
| S2 |
| 3n |
| Sn |
| 3 |
| 16 |
点评:本题考查不等式的证明,解题时要认真审题,注意等比数列的性质、放缩法的合理运用.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
定义域为R的函数f(x)满足f(x+2)=3f(x),当x∈[0,2)时,f(x)=
,若x∈[-4,-2)时,f(x)-
+
≥0恒成立,则实数t的取值范围是( )
|
| t |
| 9 |
| 2 |
| 9t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
要得到函数y=sin(2x-
)的图象,只需将函数y=sin2x的图象( )个单位.
| π |
| 6 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
集合P={x|∈Z|0≤x<3},M={x∈Z|-3≤x≤3},则P∩M=( )
| A、{1,2} |
| B、{0,1,2} |
| C、{1,2,3} |
| D、{0,1,2,3} |
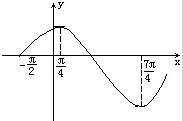 函数f(x)=sin(ωx+φ)(|φ|<
函数f(x)=sin(ωx+φ)(|φ|<