题目内容
已知函数f(x)=ax3+3x|x-2|+1,a∈R.
(Ⅰ)当a=0时,求y=f(x)的单调递增区间;
(Ⅱ)当a>0时,若函数y=f(x)不存在极值,求a的取值范围.
(Ⅰ)当a=0时,求y=f(x)的单调递增区间;
(Ⅱ)当a>0时,若函数y=f(x)不存在极值,求a的取值范围.
考点:利用导数研究函数的单调性,函数在某点取得极值的条件
专题:导数的综合应用
分析:(Ⅰ)当a=0时,f(x)=3x|x-2|,通过讨论x的范围,去掉绝对值号,从而求出单调区间;
(Ⅱ)先求出函数的导数,得到当a>0时,若函数y=f(x)不存在极值,则只能是单调递增.而当a>0时容易得3ax2+6x-6≥0对x>2恒成立;对于3ax2-6x+6≥0对x<2恒成立,则应满足
,解不等式求出即可.
(Ⅱ)先求出函数的导数,得到当a>0时,若函数y=f(x)不存在极值,则只能是单调递增.而当a>0时容易得3ax2+6x-6≥0对x>2恒成立;对于3ax2-6x+6≥0对x<2恒成立,则应满足
|
解答:
(Ⅰ)解:当a=0时,
∴f(x)=3x|x-2|+1=
,
∴y=f(x)的单调递增区间为(-∞,1),(2,+∞);
(Ⅱ)∵f(x)=ax3+3x|x-2|+1=
,
∴f′(x)=
;
∵a>0,∴3ax2+6x-6≤0在(2,+∞)不可能恒成立,
即y=f(x)不可能是单调递减.
∴当a>0时,若函数y=f(x)不存在极值,则只能是单调递增.
则有3ax2+6x-6≥0对x>2恒成立,
3ax2-6x+6≥0对x<2也恒成立.
而当a>0时容易得3ax2+6x-6≥0对x>2恒成立;
对于3ax2-6x+6≥0对x<2恒成立,
则应满足
,
或
,
得a=
,或a>
,
即a≥
.
∴f(x)=3x|x-2|+1=
|
∴y=f(x)的单调递增区间为(-∞,1),(2,+∞);
(Ⅱ)∵f(x)=ax3+3x|x-2|+1=
|
∴f′(x)=
|
∵a>0,∴3ax2+6x-6≤0在(2,+∞)不可能恒成立,
即y=f(x)不可能是单调递减.
∴当a>0时,若函数y=f(x)不存在极值,则只能是单调递增.
则有3ax2+6x-6≥0对x>2恒成立,
3ax2-6x+6≥0对x<2也恒成立.
而当a>0时容易得3ax2+6x-6≥0对x>2恒成立;
对于3ax2-6x+6≥0对x<2恒成立,
则应满足
|
或
|
得a=
| 1 |
| 2 |
| 1 |
| 2 |
即a≥
| 1 |
| 2 |
点评:本题考察了利用导数求函数的单调性,求函数的极值问题,是一道综合题.

练习册系列答案
相关题目
若曲线f(x)=sinx+1在x=π处的切线与直线ax+2y+1=0相互垂直,则实数a等于( )
| A、2 | B、1 | C、-1 | D、-2 |
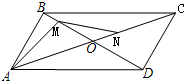 如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=
如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=