题目内容
已知函数f(x)=x2-4x+a+3,a∈R
(1)若函数y=f(x)在[-1,1]上存在零点,求a的取值范围;
(2)设函数g(x)=bx+5-2b,b∈R,当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使得f(x1)=g(x2),求b的取值范围.
(1)若函数y=f(x)在[-1,1]上存在零点,求a的取值范围;
(2)设函数g(x)=bx+5-2b,b∈R,当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使得f(x1)=g(x2),求b的取值范围.
考点:函数最值的应用,函数的零点,函数的零点与方程根的关系
专题:函数的性质及应用
分析:(1)令△≥0,f(1)•f(-1)≤0,解不等式组求得a的范围.
(2)画出两个函数的图象,根据题意知两函数图象在区间[1,4]上有交点,根据数形结合的思想求得b的范围.
(2)画出两个函数的图象,根据题意知两函数图象在区间[1,4]上有交点,根据数形结合的思想求得b的范围.
解答:
解:(1)依题意知
,求得-8≤a≤0.
(2)依题意知f(x)=x2-4x+3,图象如图,
变形g(x)=bx+5-2b得(y-5)=b(x-2),知其图象为恒过(2,5)点的直线,
依题意可知直线与抛物线在区间[1,4]上有交点,如图,
f(1)=0,f(4)=3,b为直线的斜率,
(1,0),(4,3)分别代入函数g(x)求得b分别为5,-1
以图象可知要使两函数图象在[1,4]区间上有交点需b≥5或b≤-1,
即b的范围是b≥5,或b≤-1.
|
(2)依题意知f(x)=x2-4x+3,图象如图,
变形g(x)=bx+5-2b得(y-5)=b(x-2),知其图象为恒过(2,5)点的直线,
依题意可知直线与抛物线在区间[1,4]上有交点,如图,

f(1)=0,f(4)=3,b为直线的斜率,
(1,0),(4,3)分别代入函数g(x)求得b分别为5,-1
以图象可知要使两函数图象在[1,4]区间上有交点需b≥5或b≤-1,
即b的范围是b≥5,或b≤-1.
点评:本题主要考查了函数的零点问题,直线与抛物线关系问题.第二问采用了数形结合的思想,也可采用联立方程根据零点的位置来确定b的范围.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
下列函数中,是奇函数的是( )
| A、y=xcosx |
| B、y=sin|x| |
| C、y=sinx+1 |
| D、y=|sinx| |
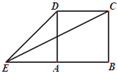 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=