题目内容
已知i是虚数单位,z=1+i,
为z的共轭复数,则复数
在复平面上对应的点的坐标为 .
. |
| z |
| z2 | ||
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:直接利用复数的除法运算化简z为a+bi(a,b∈R)的形式,则由复数的实部和虚部的符合可得答案.
解答:
解:∵z=1+i,
为z的共轭复数,
∴
=
=
=
=-1+i,
复数
在复平面上对应的点的坐标为(-1,1)
故答案为:(-1,1).
. |
| z |
∴
| z2 | ||
|
| (1+i)2 |
| 1-i |
| 2i |
| 1-i |
| 2i(1+i) |
| (1-i)(1+i) |
复数
| z2 | ||
|
故答案为:(-1,1).
点评:本题考查了复数代数形式的乘除运算,考查了复数的表示法与几何意义,是基础题.

练习册系列答案
相关题目
设函数fn=1-x+
-
+…+(-1)n
,其中n为正整数,则集合M={x|f4(x)=0,x∈R}中元素个数是( )
| x2 |
| 2 |
| x3 |
| 3 |
| xn |
| n |
| A、0个 | B、1个 | C、2个 | D、4个 |
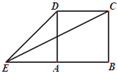 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=