题目内容
下列命题中,正确的是
①平面向量
与
的夹角为60°,
=(2,0),|
|=1,则|
+
|=
;
②已知
,
是平面内两个非零向量,则平面内任一向量
都可表示为λ
+μ
,其中λ,μ∈R;
③已知
=(sinθ,
),
=(1,
),其中θ∈(π,
),则
⊥
;
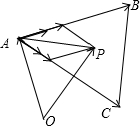
④O是△ABC所在平面上一定点,动点P满足:
=
+λ(
+
),λ∈(0,+∞),则直线AP一定通过△ABC的内心.
①平面向量
| a |
| b |
| a |
| b |
| a |
| b |
| 7 |
②已知
| a |
| b |
| c |
| a |
| b |
③已知
| a |
| 1+cosθ |
| b |
| 1-cosθ |
| 3π |
| 2 |
| a |
| b |
④O是△ABC所在平面上一定点,动点P满足:
| OP |
| OA |
| ||
|
|
| ||
|
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:①由已知可求出
•
,然后根据|
+
|=
,展开即可求解
②由平面向量的基本定理可知,
,
不能为共线向量
③把等式中
+
利用向量加法的平行四边形法则表示,由此式可知直线AP一定通过△ABC的内心.
| a |
| b |
| a |
| b |
(
|
②由平面向量的基本定理可知,
| a |
| b |
③把等式中
| ||
|
|
| ||
|
|
解答:
解:①∵向量
与
的夹角为60°,
=(2,0),|
|=1
∴
•
=|
||
|cos60°=2×1×
=1
∴|
+
|=
=
=
故①正确
由平面向量的基本定理可知,只要当
,
是平面内两个不共线的向量,则平面内任一向量
都可表示为λ
+μ
,其中λ,μ∈R,故②错误
③∵
=(sinθ,
),
=(1,
),其中θ∈(π,
)
∴
•
=sinθ×1+
=sinθ+
=sinθ-sinθ=0
∴
⊥
,故③正确
∵
=
+λ(
+
),λ∈(0,+∞),设
=
,
=
=
+λ(
+
)
-
=λ(
+
)
∴
=λ(
+
)
由向量加法的平行四边形法则可知,以
,
为邻边的平行四边形为菱形,而菱形的对角线平分对角
∴直线AP即为A的平分线所在的直线,即一定通过△ABC的内心,故④正确
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| 1 |
| 2 |
∴|
| a |
| b |
(
|
|
=
| 4+2+1 |
| 7 |
故①正确
由平面向量的基本定理可知,只要当
| a |
| b |
| c |
| a |
| b |
③∵
| a |
| 1+cosθ |
| b |
| 1-cosθ |
| 3π |
| 2 |
∴
| a |
| b |
| (1+cosθ)(1-cosθ) |
| 1-cos2θ |
∴
| a |
| b |
∵
| OP |
| OA |
| ||
|
|
| ||
|
|
| e1 |
| ||
|
|
| e2 |
| ||
|
|
=
| OA |
| e1 |
| e2 |
| OP |
| OA |
| e1 |
| e2 |
∴
| AP |
| e1 |
| e2 |
由向量加法的平行四边形法则可知,以
| e1 |
| e2 |
∴直线AP即为A的平分线所在的直线,即一定通过△ABC的内心,故④正确

点评:本题主要考查了命题真假关系的判断,解答④的关键是需要知道
是
方向上的单位向量
| ||
|
|
| a |

练习册系列答案
相关题目
已知复数z满足(z-1)(1+2i)=2i(i为虚数单位),则z的虚部是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:?x∈R,lnx+x-2=0,命题q:?x∈R,2x≥x2,则下列命题中为真命题的是( )
| A、p∧q | B、¬p∧q |
| C、p∧¬q | D、¬p∧¬q |
 如图,设G、H分别为△ABC的重心、垂心,F为线段GH的中点,若△ABC外接圆的半径为1,则|
如图,设G、H分别为△ABC的重心、垂心,F为线段GH的中点,若△ABC外接圆的半径为1,则|