题目内容
等差数列{an}中,若a2+a8=15-a5,则a5的值为( )
| A、3 | B、4 | C、5 | D、6 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由等差数列的性质化简已知的式子,从而求出a5的值.
解答:
解:由题意得,a2+a8=15-a5,
所以由等差数列的性质得a2+a8=2a5=15-a5,
解得a5=5,
故选:C.
所以由等差数列的性质得a2+a8=2a5=15-a5,
解得a5=5,
故选:C.
点评:本题考查等差数列的性质的灵活应用,属于基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,则该程序运行后输出的k的值是( )


| A、3 | B、4 | C、5 | D、6 |
已知an=n+2,bn=2n-3,则数列{anbn}的前n项和Sn等于( )
A、(n+2)•2n-1-
| ||
B、
| ||
C、(n+1)•2n-2-
| ||
D、
|
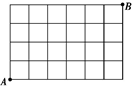 某市新城区有7条南北向街道,5条东西向街道(如图).
某市新城区有7条南北向街道,5条东西向街道(如图).