题目内容

若集合M={y|y=3x}，集合S={x|y=lg（x-1）}，则下列各式正确的是（　　）
A、M∪S=MB、M∪S=S
C、M=SD、M∩S=∅
考点：补集及其运算
专题：集合
分析：由指数函数的值域、对数函数的定义域分别求出集合M、N，然后逐个判断即可．
解答： 解：M={y|y＞0}，S={x|x＞1}，
∴M∪S={y|y＞0}=N．
故选A．
点评：本题主要考查指数函数的值域、对数函数的定义域和集合间的运算，属于基础题．
练习册系列答案
相关题目
△ABC所在平面α外一点P到三角形三顶点的距离相等，那么点P在α内的射影一定是△ABC的
 
心（填“内”、”外”、“重”、“垂”）．
已知椭圆C的上、下顶点分别为B1、B2，左、右焦点分别为F1、F2，若四边形B1F1B2F2是正方形，则此椭圆的离心率e等于（　　）
A、
1
3
B、
1
2
C、
2
2
D、
3
2
棱长为1的正方体各顶点都在同一个球面上，则该球面的表面积等于（　　）
A、2π
B、
3π
2
C、3π
D、4π
有四个关于三角函数的命题：
p1：?x∈R，使得sinx+cosx=
3
2
；
p2：?x，y∈R，使得sin（x+y）=sinx+siny；
p3：?x∈[0，π]，都有
1-cos2x
2
=sinx；
p4：任意锐角△ABC中，恒有sinA＞cosB成立；
其中真命题的个数是（　　）
A、1B、2C、3D、4
设变量x，y满足约束条件
y≥0
x-y+1≥0
x+y-3≤0
．若目标函数z=ax+y在点（1，2）处取得最大值，则a的取值范围为（　　）
A、（1，+∞）
B、（-∞，-1）
C、（-1，1）
D、[-1，1]
函数y=
1
x1-m
在第二象限内单调递增，则m的最大负整数是（　　）
A、-4B、-3C、-2D、-1
已知函数f（x）=sinxcosx+
3
cos2x-
3
2
（x∈R）．
（1）写出f（x）的最小正周期及最大值；
（2）求f（x）的增区间．
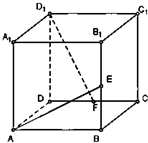如图，在正方体ABCD-A1B1C1D1中，E、F分别是BB1、DC的中点．
（Ⅰ）求异面直线AE与D1F所成的角；
（Ⅱ）证明：AE⊥平面A1D1F．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网