题目内容
下列函数中,既是奇函数又在[-1,1]上是单调递减的函数是( )
| A、f(x)=sinx | ||
| B、f(x)=-|x-1| | ||
C、f(x)=
| ||
D、f(x)=ln
|
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:本题是选择题,可采用逐一检验的方法,只要不满足其中一条就能说明不正确.
解答:
解:f(x)=sinx是奇函数,但其在区间[-1,1]上单调递增,故A错;
∵f(x)=-|x-1|,∴f(-x)=-|-x-1|≠-f(x),∴f(x)=-|x+1|不是奇函数,∴故B错;
∵a>1时,y=ax在[-1,1]上单调递增,y=a-x[-1,1]上单调递减,∴f(x)=
(ax+a-x)(a>0,a≠1)在[-1,1]上单调递增,故C错;
故选:D.
∵f(x)=-|x-1|,∴f(-x)=-|-x-1|≠-f(x),∴f(x)=-|x+1|不是奇函数,∴故B错;
∵a>1时,y=ax在[-1,1]上单调递增,y=a-x[-1,1]上单调递减,∴f(x)=
| 1 |
| 2 |
故选:D.
点评:题综合考查了函数的奇偶性与单调性,本选择题要直接利用函数奇偶性的性质对选项逐一检验的方法,本类题是函数这一部分的常见好题.

练习册系列答案
相关题目
若A={(2,-2),(2,2)},则集合A中元素的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
集合M中的元素都是正整数,且若a∈M,则6-a∈M,则所有满足条件的集合M共有( )
| A、6个 | B、7个 | C、8个 | D、9个 |
函数y=
在第二象限内单调递增,则m的最大负整数是( )
| 1 |
| x1-m |
| A、-4 | B、-3 | C、-2 | D、-1 |
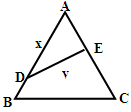 如图,公园有一块边长为2的等边的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域.
如图,公园有一块边长为2的等边的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域.