题目内容
已知sinθ-cosθ=
，则cos（
-2θ）= ．
| 1 |
| 3 |
| π |
| 2 |
考点：二倍角的正弦,运用诱导公式化简求值
专题：计算题,三角函数的求值
分析：将已知等式两边平方，利用完全平方公式及同角三角函数间的基本关系化简，再利用二倍角的正弦函数公式化简求出sin2θ的值，即可得出结论．
解答：
解：将sinθ-cosθ=
两边平方得：
（sinθ-cosθ）2=sin2θ-2sinθcosθ+cos2θ=1-sin2θ=
，
∴sin2θ=
，
∴cos（
-2θ）=sin2θ=
，
故答案为：
．
| 1 |
| 3 |
（sinθ-cosθ）2=sin2θ-2sinθcosθ+cos2θ=1-sin2θ=
| 1 |
| 9 |
∴sin2θ=
| 8 |
| 9 |
∴cos（
| π |
| 2 |
| 8 |
| 9 |
故答案为：
| 8 |
| 9 |
点评：此题考查了二倍角的正弦函数公式，以及同角三角函数间的基本关系，熟练掌握公式是解本题的关键．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
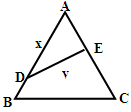如图，公园有一块边长为2的等边的三角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．设AD=x（x≥0），DE=y，求用x表示y的函数关系式，并求函数的定义域．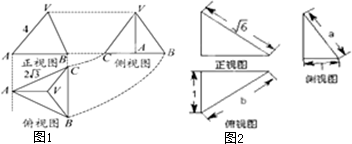
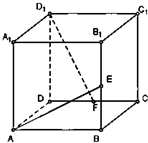如图，在正方体ABCD-A1B1C1D1中，E、F分别是BB1、DC的中点．