题目内容

若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则此几何体的体积等于（　　）
A、30B、12C、24D、4
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：三视图复原的几何体是三棱柱去掉一个三棱锥的几何体，结合三视图的数据，求出体积即可．
解答： 解：由三视图知几何体是底面为边长为3，4，5的三角形，高为5的三棱柱被平面截得的，
如图所示，
所以几何体的体积为：
1
2
×3×4×5-
1
3
×
1
2
×3×4×3=24．
故选：C．
点评：本题考查三视图的识别以及多面体的体积问题．根据三视图得出几何体的形状及长度关系是解决问题的关键．
练习册系列答案
相关题目
证明不等式：如果a，b都是正数，且a≠b，求证：
a
b
+
b
a
＞
a
+
b
．
用适当的符号填空：
（1）0
 
{x|x2=0}，
（2）∅
 
{x∈R|x2+1=0}，
（3）{0，1}
 
N．
若a=n2+1，n∈N，A={x|x=k2-4k+5，k∈N}，则a与A的关系是
 
．
已知函数f（x）=
1
2
sin（ax+
2π
7
）的最小正周期为4π，则正实数a=
 
．
已知椭圆C的上、下顶点分别为B1、B2，左、右焦点分别为F1、F2，若四边形B1F1B2F2是正方形，则此椭圆的离心率e等于（　　）
A、
1
3
B、
1
2
C、
2
2
D、
3
2
若A={（2，-2），（2，2）}，则集合A中元素的个数是（　　）
A、1个B、2个C、3个D、4个
有四个关于三角函数的命题：
p1：?x∈R，使得sinx+cosx=
3
2
；
p2：?x，y∈R，使得sin（x+y）=sinx+siny；
p3：?x∈[0，π]，都有
1-cos2x
2
=sinx；
p4：任意锐角△ABC中，恒有sinA＞cosB成立；
其中真命题的个数是（　　）
A、1B、2C、3D、4
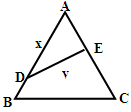如图，公园有一块边长为2的等边的三角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．设AD=x（x≥0），DE=y，求用x表示y的函数关系式，并求函数的定义域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网