题目内容
11．已知直线a和平面α，则平面α内必有一直线与直线a垂直（从“相交，平行，异面，垂直”中选填）．分析 由题意分a?α，a∥α，a与α相交三种情况得到平面α内直线与a的位置关系得答案．
解答 解：若a?α，则平面α内必有一直线与直线a平行或相交或垂直；
若a∥α，则平面α内必有一直线与直线a平行或异面或垂直；
若a与α相交，则平面α内必有一直线与直线a相交或垂直或异面．
则平面α内必有一直线与直线a垂直．
故答案为：垂直．
点评 本题考查空间中直线与直线、直线与平面的位置关系，考查空间想象能力和思维能力，属中档题．
练习册系列答案
相关题目
2．已知函数f（x）的图象关于（1，1）对称，当x∈（0，1]时，f（x）=x2，当x∈（-1，0]时，f（x）+2=$\frac{2}{f（\sqrt{x+1}）}$，若g（x）=f（x）-t（x+1）为定义在（-1，3）上的函数，则关于g（x）的零点个数的叙述中错误的是（ ）
| A． | g（x）可能没有零点 | B． | g（x）可能有1个零点 | C． | g（x）可能有2个零点 | D． | g（x）可能有3个零点 |
6．有4个不同的球，四个不同的盒子，把球全部放入盒内，恰有两个盒不放球，共有（ ）种放法．
| A． | 114 | B． | 96 | C． | 84 | D． | 48 |
16．设实数x，y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}\right.$，则z=$\frac{4x}{y}$+$\frac{y}{x}$的取值范围是（ ）
| A． | [4，$\frac{17}{2}$] | B． | [$\frac{13}{3}$，$\frac{17}{2}$] | C． | [4，$\frac{37}{3}$] | D． | [$\frac{17}{2}$，$\frac{37}{3}$] |
3．
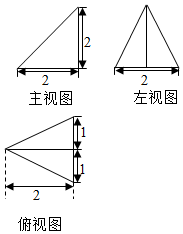已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得出这个几何体的内切球半径是（ ）
已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得出这个几何体的内切球半径是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{4}{9}$ | C． | $\sqrt{6}-2$ | D． | $3\sqrt{6}-6$ |
20．已知数列{an}的前n项和是Sn，则下列四个命题中，错误的是（ ）
| A． | 若数列{an}是公差为d的等差数列，则数列{$\frac{{S}_{n}}{n}$}的公差为$\frac{d}{2}$的等差数列 | |
| B． | 若数列{$\frac{{S}_{n}}{n}$}是公差为d的等差数列，则数列{an}是公差为2d的等差数列 | |
| C． | 若数列{an}是等差数列，则数列的奇数项，偶数项分别构成等差数列 | |
| D． | 若数列{an}的奇数项，偶数项分别构成公差相等的等差数列，则{an}是等差数列 |