题目内容
20．已知数列{an}的前n项和是Sn，则下列四个命题中，错误的是（ ）| A． | 若数列{an}是公差为d的等差数列，则数列{$\frac{{S}_{n}}{n}$}的公差为$\frac{d}{2}$的等差数列 | |
| B． | 若数列{$\frac{{S}_{n}}{n}$}是公差为d的等差数列，则数列{an}是公差为2d的等差数列 | |
| C． | 若数列{an}是等差数列，则数列的奇数项，偶数项分别构成等差数列 | |
| D． | 若数列{an}的奇数项，偶数项分别构成公差相等的等差数列，则{an}是等差数列 |
分析 根据等差数列的通项公式和前n项和公式进行分析，并作出判断．
解答 解：A、若等差数列{an}的首项为a1，公差为d，前n项的和为Sn，则数列{$\frac{{S}_{n}}{n}$}为等差数列，且通项为$\frac{{S}_{n}}{n}$=a1+（n-1）$\frac{d}{2}$，即数列{$\frac{{S}_{n}}{n}$}的公差为$\frac{d}{2}$的等差数列，故说法正确；
B、由题意得：$\frac{{S}_{n}}{n}$=a1+（n-1）d，所以Sn=na1+n（n-1）d，则an=Sn-Sn-1=a1+2（n-1）d，即数列{an}是公差为2d的等差数列，故说法正确；
C、若数列{an}是等差数列的公差为d，则数列的奇数项，偶数项都是公差为2d的等差数列，说法正确；
D、若数列{an}的奇数项，偶数项分别构成公差相等的等差数列，则{an}不一定是等差数列，例如：{1，4，3，6，5，8，7}，说法错误．
故选：D．
点评 本题考查等差数列的性质，考查等差数列的求和公式，考查运算与推理、证明的能力，属于中档题．
练习册系列答案
相关题目
8．
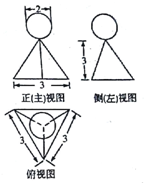某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{4π}{3}$+$\frac{9\sqrt{3}}{4}$ | B． | $\frac{4π}{3}$+$\frac{27\sqrt{3}}{4}$ | C． | $\frac{8π}{3}$+$\frac{9\sqrt{3}}{4}$ | D． | $\frac{8π}{3}$+$\frac{27\sqrt{3}}{4}$ |
已知一个几何体的三视图如图所示（单位：cm）．则该几何体的体积为8πcm3．
9．
已知f（x）=Asin （ω x+φ）+（A＞0，ω＞0，|φ|＜π}）的图象如图所示，则f（3π）=（ ）
已知f（x）=Asin （ω x+φ）+（A＞0，ω＞0，|φ|＜π}）的图象如图所示，则f（3π）=（ ）| A． | -$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |