题目内容
16.设实数x,y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}\right.$,则z=$\frac{4x}{y}$+$\frac{y}{x}$的取值范围是( )| A. | [4,$\frac{17}{2}$] | B. | [$\frac{13}{3}$,$\frac{17}{2}$] | C. | [4,$\frac{37}{3}$] | D. | [$\frac{17}{2}$,$\frac{37}{3}$] |
分析 首先画出可行域,利用目标函数的几何意义求z的最值.
解答 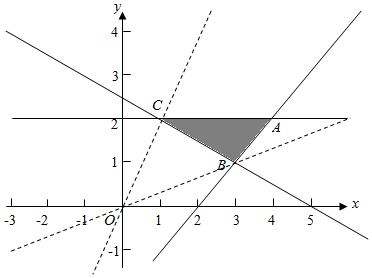 解:由已知得到可行域如图:由图象得到$\frac{y}{x}$的范围为[kOB,kOC],即[$\frac{1}{3}$,2],
解:由已知得到可行域如图:由图象得到$\frac{y}{x}$的范围为[kOB,kOC],即[$\frac{1}{3}$,2],
所以z=$\frac{4x}{y}$+$\frac{y}{x}$的最小值为4;(当且仅当y=2x=2时取得);
当$\frac{y}{x}$=$\frac{1}{3}$,z 最大值为$4×3+\frac{1}{3}=\frac{37}{3}$;
所以z=$\frac{4x}{y}$+$\frac{y}{x}$的取值范围是[4,$\frac{37}{3}$];
故选:C.
点评 本题考查了简单线性规划问题;关键是正确画出可行域,利用$\frac{y}{x}$目标函数的几何意义求出其最值,然后根据对勾函数的性质求z 的范围.

练习册系列答案
相关题目
13.某校为了解学生对数学学案质量的满意度,从高一、高二两个年级分别随机调查了20个学生,得到对学案满意度评分(满分100分)的茎叶图如图:则下列说法错误的是( )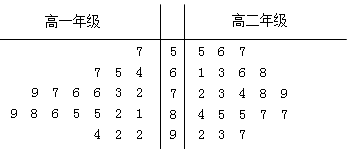

| A. | 高一学生满意度评分的平均值比高二学生满意度评分的平均值高 | |
| B. | 高一学生满意度评分比较集中,高二学生满意度评分比较分散 | |
| C. | 高一学生满意度评分的中位数为80 | |
| D. | 高二学生满意度评分的中位数为74 |
7.向边长为1的正方形内随机投一粒豆子,则豆子到正方形的顶点A的距离不大于$\frac{1}{2}$的概率是( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{π}$ | D. | $\frac{π}{16}$ |
8.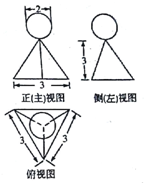 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4π}{3}$+$\frac{9\sqrt{3}}{4}$ | B. | $\frac{4π}{3}$+$\frac{27\sqrt{3}}{4}$ | C. | $\frac{8π}{3}$+$\frac{9\sqrt{3}}{4}$ | D. | $\frac{8π}{3}$+$\frac{27\sqrt{3}}{4}$ |
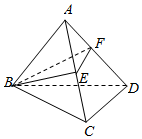 如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.
如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.