题目内容
19.已知ρ:|1-$\frac{x-1}{3}$|≤2,q:(x-1+m)(x-1-m)≤0(m>0),若q是p充分不必要条件,求实数m的取值范围.分析 先分别求得p,q所对应的集合,再根据q是p的充分不必要条件,可求实数m的取值范围.
解答 解:由:|1-$\frac{x-1}{3}$|≤2,得-2≤x≤10,
∵m>0,∴1+m>1-m
∴由[x-(1+m)][x-(1-m)]≤0,
得:1-m≤x≤1+m
因为q是p的充分不必要条件,
所以$\left\{\begin{array}{l}{1-m≥-2}\\{1+m≤10}\\{m>0}\end{array}\right.$,∴0<m≤3,
故实数m的取值范围是(0,3].
点评 本题以集合为载体,考查四种条件,解不等式,利用q是p的充分不必要条件,构建不等式组是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.某椎体的三视图如图所示,则该棱锥的最长棱的棱长为( )
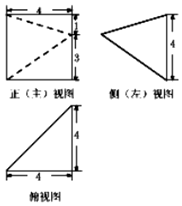

| A. | $\sqrt{33}$ | B. | $\sqrt{17}$ | C. | $\sqrt{41}$ | D. | $\sqrt{42}$ |
7.已知复数z满足$\frac{1-i}{\overline{z}}$=i(其中i为虚数单位),则z2=( )
| A. | 2i | B. | -2i | C. | 2+2i | D. | 2-2i |
8.现有7名数理化成绩优秀者,分别用A1,A2,A3,B1,B2,C1,C2表示,其中A1,A2,A3的数学成绩优秀,B1,B2的物理成绩优秀,C1,C2的化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛,则A1或B1仅一人被选中的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
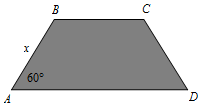 无锡市要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计基横断面要求面积为$6\sqrt{3}$平方米,且高度不低于$\sqrt{3}$米,记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).
无锡市要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计基横断面要求面积为$6\sqrt{3}$平方米,且高度不低于$\sqrt{3}$米,记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).