题目内容
9.已知数列{an}的前n项和Sn=$\frac{3}{2}$an-$\frac{1}{2}$(1)求a1
(2)求{an}的通项公式及其前n项和Tn.
分析 (1)依题意知,a1=S1,S1=$\frac{3}{2}$a1-$\frac{1}{2}$,据此求得a1;
(2)利用等比数列的定义推知数列{an}是一个以1为首项,3为公比的等比数列,所以结合等比数列的前n项和公式解答即可.
解答 解:(1)由S1=$\frac{3}{2}$a1-$\frac{1}{2}$且a1=S1,得a1=1;
(2)∵当n≥2时,an=Sn-Sn-1=$\frac{3}{2}$an-$\frac{3}{2}$an-1,
∴$\frac{3}{2}$an-1=$\frac{1}{2}$an,
∴an=3an-1,(n≥2).
∴{an}是一个以1为首项,3为公比的等比数列
∴an=3n-1,
∴Tn.=$\frac{1}{2}$(3n-1).
点评 本题主要考查数列通项公式和前n项和的求解,掌握等比数列的定义和等比数列的前n项和公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.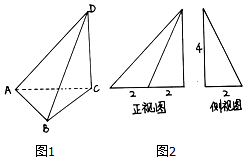 三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
 三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )| A. | 32π | B. | 36π | C. | 128π | D. | 144π |
19. 将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )
将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )
 将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )
将正方体切去一个三棱锥得到几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{22}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{16}{3}$ | D. | 6 |

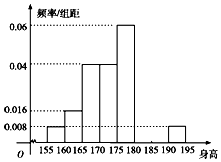 从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.
从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.