题目内容
20.某椎体的三视图如图所示,则该棱锥的最长棱的棱长为( )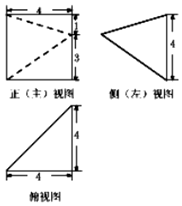
| A. | $\sqrt{33}$ | B. | $\sqrt{17}$ | C. | $\sqrt{41}$ | D. | $\sqrt{42}$ |
分析 画出三视图对应的几何体的图形,说明几何体的形状,然后求解棱长即可.
解答  解:该几何体为一个侧面与底面垂直,底面为正方形的四棱锥(如图所示),其中底面ABCD边长为4,侧面PAD⊥平面ABCD,点P在底面的射影为E,所以PE⊥AD,DE=1,AE=4,PE=4,所以$PA=\sqrt{P{E^2}+A{E^2}}=5$,$PB=\sqrt{P{E^2}+B{E^2}}=\sqrt{41}$,$PC=\sqrt{P{E^2}+C{E^2}}=\sqrt{33}$,
解:该几何体为一个侧面与底面垂直,底面为正方形的四棱锥(如图所示),其中底面ABCD边长为4,侧面PAD⊥平面ABCD,点P在底面的射影为E,所以PE⊥AD,DE=1,AE=4,PE=4,所以$PA=\sqrt{P{E^2}+A{E^2}}=5$,$PB=\sqrt{P{E^2}+B{E^2}}=\sqrt{41}$,$PC=\sqrt{P{E^2}+C{E^2}}=\sqrt{33}$,
$PD=\sqrt{P{E^2}+D{E^2}}=\sqrt{17}$,底面边长为4,所以最长的棱长为$\sqrt{41}$,
故选:C.
点评 本题考查空间几何体的点线面距离的求法,三视图与几何体的关系,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
11.直线x=a分别与曲线y=2(x+1),y=x+lnx交于A、B两点,则|AB|的最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{3}{2}$ |
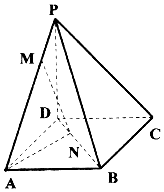 如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.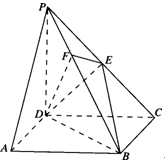 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.