题目内容
8.现有7名数理化成绩优秀者,分别用A1,A2,A3,B1,B2,C1,C2表示,其中A1,A2,A3的数学成绩优秀,B1,B2的物理成绩优秀,C1,C2的化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛,则A1或B1仅一人被选中的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
分析 先求出基本事件总数n=3×2×2=12,再求出A1或B1仅一人被选中包含的基本事件个数m=1×1×2+2×1×2=6,由此能求出A1或B1仅一人被选中的概率.
解答 解:现有7名数理化成绩优秀者,分别用A1,A2,A3,B1,B2,C1,C2表示,
其中A1,A2,A3的数学成绩优秀,B1,B2的物理成绩优秀,C1,C2的化学成绩优秀.
从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛,
基本事件总数n=3×2×2=12,
A1或B1仅一人被选中包含的基本事件个数m=1×1×2+2×1×2=6,
∴A1或B1仅一人被选中的概率为p=$\frac{m}{n}$=$\frac{6}{12}=\frac{1}{2}$.
故选:C.
点评 本题考查概率的求法,考查学生分析解决问题的能力,考查数据处理能力、运算求解能力,属于基础题.

练习册系列答案
相关题目
18.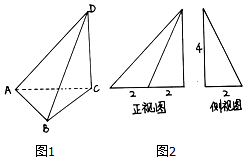 三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
 三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )
三棱锥D-ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( )| A. | 32π | B. | 36π | C. | 128π | D. | 144π |
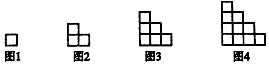 如图图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第15个图形中小正方形的个数是120.
如图图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第15个图形中小正方形的个数是120.